
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的面积记作S2 , 照此规律作下去,则S1= , S2017= . 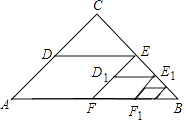
【答案】1;![]()
【解析】解:∵∠C=90°,AC=BC=2,
∴△ABC的面积为: ![]() ×2×2=2,
×2×2=2,
∵点E为BC边中点,ED∥AB,
∴△CDE∽△CAB,
∴ ![]() =
= ![]() ,
,
∴S△CDE= ![]() ,
,
∵EF∥AC,点E为BC边中点,
∴S△BEF= ![]() ,
,
∴S1=1,
同理,S2= ![]() ,S3=
,S3= ![]() ,
,
以此类推,S2017= ![]() .
.
所以答案是:1; ![]() .
.
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
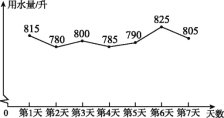

(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
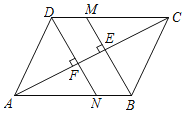
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有
①∠A+∠B=90°
②AB2=AC2+BC2
③ ![]()
④CD2=ADBD.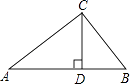
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 ![]() 的概率是 .
的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进![]() ,
,![]() 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,![]() 型号机器人的单价比
型号机器人的单价比![]() 型号机器人贵600元,3台
型号机器人贵600元,3台![]() 型号机器人比2台
型号机器人比2台![]() 型号机器人贵1200元.
型号机器人贵1200元.
(1)求![]() ,
,![]() 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?
(2)若该快递公司准备用不超过132000元购进![]() ,
,![]() 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进![]() 型号机器人多少台?
型号机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com