
【题目】阅读材料:善于思考的小军在解方程组 时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
把方程①带入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程组的解为![]() .
.
请你解决以下问题:(1)模仿小军的“整体代换”法解方程组 ;
;
(2)已知x,y满足方程组 .
.
(i)求![]() 的值;
的值;
(ii)求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法: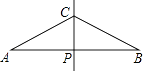
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
A.甲、乙都正确
B.甲、乙都错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 对角线相等的四边形是矩形
B. 对角线互相垂直平分的四边形是菱形
C. 一组对边平行,另一组对边相等的四边形是平行四边形
D. 一组邻边相等,并且有一个内角为直角的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=120°时,∠AEB′= °;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投掷一枚普通的正方体骰子24次。
(1)你认为下列四种说法哪种是正确的?①出现1点的概率等于出现3点的概率;
②投掷24次,2点一定会出现4次;
③投掷前默念几次“出现4点”,投掷结果出现4点的可能性就会加大;
④连续投掷6次,出现的点数之和不可能等于37。
(2)求出现5点的概率;
(3)出现6点大约有多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识迁移
我们知道,函数![]() 的图像是由二次函数
的图像是由二次函数![]() 的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数
的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数![]() 的图像是由反比例函数
的图像是由反比例函数![]() 的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
理解应用
函数![]() 的图像可以由函数
的图像可以由函数![]() 的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
灵活运用
如图,在平面直角坐标系xOy中,请根据所给的![]() 的图像画出函数
的图像画出函数![]() 的图像,并根据该图像指出,当x在什么范围内变化时,
的图像,并根据该图像指出,当x在什么范围内变化时,![]() ≥
≥![]() ?
?
实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为![]() ;若在
;若在![]() (
(![]() ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为![]() .如果记忆存留量为
.如果记忆存留量为![]() 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com