
 将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,求CD的长.
将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,求CD的长. 分析 根据旋转的性质得AD=AB,由∠B=60°,于是可判断△ADB为等边三角形,根据等边三角形的性质得BD=AB=1,然后利用CD=BC-BD进行计算.
解答 解:∵∠B=60°,
∴∠C=90°-60°=30°,
∵AC=$\sqrt{3}$,
∴AC2+AB2=BC2,即($\sqrt{3}$)2+AB2=4AB2,
∴AB=1、BC=2AB=2,
由旋转的性质知,AB=AD,
∴△ABD是等边三角形,
∴BD=AB=1,
则CD=BC-BD=2-1=1.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.


科目:初中数学 来源: 题型:填空题
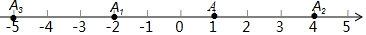 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
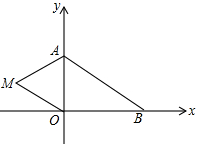 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
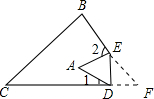 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | α=135°+$\frac{β+γ}{2}$ | B. | γ>β+45° | ||
| C. | ∠β与∠γ有可能互补 | D. | α+β+γ<270° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com