
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌвбжЊЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() жБЯп
жБЯп![]() ЃЌ
ЃЌ![]() жБЯп
жБЯп![]() ЃЌДЙзуЗжБ№ЮЊЕу
ЃЌДЙзуЗжБ№ЮЊЕу![]() ЁЂ
ЁЂ![]() ЃЎжЄУїЃК
ЃЎжЄУїЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЖМдкжБЯп
Ш§ЕуЖМдкжБЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊШЮвтШёНЧЛђЖлНЧЃЎЧыЮЪНсТл
ЮЊШЮвтШёНЧЛђЖлНЧЃЎЧыЮЪНсТл![]() ЪЧЗёШдШЛГЩСЂЃПШчГЩСЂЃЛЧыФуИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёШдШЛГЩСЂЃПШчГЩСЂЃЛЧыФуИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЭиеЙгыгІгУЃКШчЭМЃЈ3ЃЉЃЌ![]() ЁЂ
ЁЂ![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФСНЖЏЕу
ЩЯЕФСНЖЏЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЛЅВЛжиКЯЃЉЃЌЕу
Ш§ЕуЛЅВЛжиКЯЃЉЃЌЕу![]() ЮЊ
ЮЊ![]() ЦНЗжЯпЩЯЕФвЛЕуЃЌЧв
ЦНЗжЯпЩЯЕФвЛЕуЃЌЧв![]() КЭ
КЭ![]() ОљЮЊЕШБпШ§НЧаЮЃЌСЌНг
ОљЮЊЕШБпШ§НЧаЮЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉГЩСЂЃЛжЄУїМћНтЮіЃЛЃЈ3ЃЉжЄУїМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬѕМўПЩжЄУїЁїABDЁеЁїCAEЃЌПЩЕУDA=CEЃЌAE=BDЃЌПЩЕУDE=BD+CEЃЛ
ЃЈ2ЃЉгЩЬѕМўПЩжЊЁЯBAD+ЁЯCAE=180Ёу-ІСЃЌЧвЁЯDBA+ЁЯBAD=180Ёу-ІСЃЌПЩЕУЁЯDBA=ЁЯCAEЃЌНсКЯЬѕМўПЩжЄУїЁїABDЁеЁїCAEЃЌЭЌЃЈ1ЃЉПЩЕУГіНсТлЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌЁїADBЁеЁїCAEЃЌЕУЕНBD=EAЃЌЁЯDBA=ЁЯCAEЃЌжЄУїЁїDBFЁеЁїEAFЃЈSASЃЉЃЌЕУЕНDF=EFЃЎ
ЃЈ1ЃЉЁпBDЁЭlЃЌCEЁЭlЃЌ
ЁрЁЯBDA=ЁЯAEC=90Ёу
гжЁпЁЯBAC=90ЁуЃЌ
ЁрЁЯBAD+ЁЯCAE=90ЁуЃЌЁЯBAD+ЁЯABD=90ЁуЃЌ
ЁрЁЯCAE=ЁЯABD
дкЁїABDКЭЁїCAEжаЃЌ
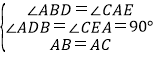 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїCAEЃЈAASЃЉ
ЁрBD=AEЃЌAD=CEЃЌ
ЁпDE=AD+AEЃЌ
ЁрDE=CE+BDЃЛ
ЃЈ2ЃЉГЩСЂ
ЁпЁЯBDA=ЁЯAEC=ЁЯBAC=ІСЃЌ
ЁрЁЯDBA+ЁЯBAD=ЁЯBAD+ЁЯCAE=180Ёу-ІСЃЌ
ЁрЁЯCAE=ЁЯABDЃЌ
дкЁїADBКЭЁїCEAжаЃЌ
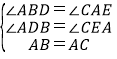 ЃЌ
ЃЌ
ЁрЁїADBЁеЁїCEAЃЈAASЃЉЃЌ
ЁрAE=BDЃЌAD=CEЃЌ
ЁрBD+CE=AE+AD=DEЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌЁїADBЁеЁїCAEЃЌ
ЁрBD=EAЃЌЁЯDBA=ЁЯCAEЃЌ
ЁпЁїABFКЭЁїACFОљЮЊЕШБпШ§НЧаЮЃЌ
ЁрЁЯABF=ЁЯCAF=60ЁуЃЌ
ЁрЁЯDBA+ЁЯABF=ЁЯCAE+ЁЯCAFЃЌ
ЁрЁЯDBF=ЁЯFAEЃЌ
ЁпBF=AF
дкЁїDBFКЭЁїEAFжаЃЌ
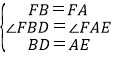 ЃЌ
ЃЌ
ЁрЁїDBFЁеЁїEAFЃЈSASЃЉЃЌ
ЁрDF=EF.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌИјГіСЫИёЕуЁїABCЁЂжБЯпlКЭИёЕуOЃЎ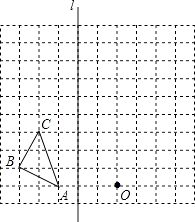
ЂйЛГіЁїABCЙигкжБЯпlГЩжсЖдГЦЕФЁїA0B0C0ЃЛ
ЂкЛГіНЋЁїA0B0C0ЯђЩЯЦНвЦ1ИіЕЅЮЛЕУЕНЕФЁїA1B1C1ЃЛ
ЂлвдИёЕуOЮЊЮЛЫЦжааФЃЌНЋЁїA1B1C1зїЮЛЫЦБфЛЛЃЌНЋЦфЗХДѓЕНдРДЕФСНБЖЃЌЕУЕНЁїA2B2C2 ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
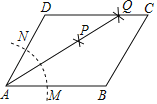
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌАДвдЯТВНжшзїЭМЃКЂйвдAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїЛЁЃЌЗжБ№НЛABЃЌADгкЕуMЃЌNЃЛЂкЗжБ№вдMЃЌNЮЊдВаФЃЌвдДѓгк![]() MNЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуPЃЛЂлзїAPЩфЯпЃЌНЛБпCDгкЕуQЃЌШєDQ=2QCЃЌBC=3ЃЌдђЦНааЫФБпаЮABCDжмГЄЮЊ________ЃЎ
MNЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуPЃЛЂлзїAPЩфЯпЃЌНЛБпCDгкЕуQЃЌШєDQ=2QCЃЌBC=3ЃЌдђЦНааЫФБпаЮABCDжмГЄЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪпВЫЩњВњЛљЕидкЦјЮТНЯЕЭЪБЃЌгУзАгаКуЮТЯЕЭГЕФДѓХяддХрвЛжждкздШЛЙтееЧвЮТЖШЮЊ18ЁцЕФЬѕМўЯТЩњГЄзюПьЕФаТЦЗжжЃЌЯТЭМЪЧФГЬьКуЮТЯЕЭГДгПЊЦєЕНЙиБеМАЙиБеКѓЃЌДѓХяФкЮТЖШyЃЈЁцЃЉЫцЪБМфxЃЈаЁЪБЃЉБфЛЏЕФКЏЪ§ЭМЯѓЃЌЦфжаBCЖЮЪЧЫЋЧњЯпy=![]() ЕФвЛВПЗжЃЎЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
ЕФвЛВПЗжЃЎЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉКуЮТЯЕЭГдкетЬьБЃГжДѓХяФкЮТЖШ18ЁцЕФЪБМфгаЖрЩйаЁЪБЃП
ЃЈ2ЃЉЧѓkЕФжЕЃЛ
ЃЈ3ЃЉЕБx=18ЪБЃЌДѓХяФкЕФЮТЖШдМЮЊЖрЩйЖШЃП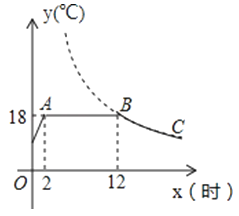
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDЖЅЕуAЁЂBдкxжсЩЯЃЌЕуDдкyжсЩЯЃЌКЏЪ§y= ![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуCЃЈ2ЃЌ3ЃЉЃЌжБЯпADНЛЫЋЧњЯпгкЕуEЃЌВЂЧвEBЁЭxжсЃЌCDЁЭyжсЃЌEBгыCDНЛгкЕуFЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуCЃЈ2ЃЌ3ЃЉЃЌжБЯпADНЛЫЋЧњЯпгкЕуEЃЌВЂЧвEBЁЭxжсЃЌCDЁЭyжсЃЌEBгыCDНЛгкЕуFЃЎ
ЃЈ1ЃЉШєEB= ![]() ODЃЌЧѓЕуEЕФзјБъЃЛ
ODЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉШєЫФБпаЮABCDЮЊЦНааЫФБпаЮЃЌЧѓЙ§AЁЂDСНЕуЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБпЁїABCЕФБпГЄЮЊ2ЃЌCDЮЊABБпЩЯЕФжаЯпЃЌEЮЊЯпЖЮCDЩЯЕФЖЏЕуЃЌвдBEЮЊБпЃЌдкBEзѓВрзїЕШБпЁїBEFЃЌСЌНгDFЃЌдђDFЕФзюаЁжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
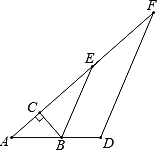
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїADEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃНЁЯDAEЃН90ЁуЃЌBЁЂCЁЂEШ§ЕуЙВЯпЃЌСЌНгDCЃЌЕуFЮЊCDЩЯЕФвЛЕуЃЌСЌНгAFЃЎ
ЃЈ1ЃЉШєBEЦНЗжЁЯAEDЃЌЧѓжЄЃКACЃНECЃЛ
ЃЈ2ЃЉШєЁЯDAFЃНЁЯAECЃЌЧѓжЄЃКBEЃН2AFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯA=40ЁуЃЌЁїABCЕФЭтНЧЁЯCBDЕФЦНЗжЯпBEНЛACЕФбгГЄЯпгкЕуEЃЌЕуFЮЊACбгГЄЯпЩЯЕФвЛЕуЃЌСЌНгDF.
(1)ЧѓЁЯCBEЕФЖШЪ§ЃЛ
(2)ШєЁЯF=25Ёу,ЧѓжЄ:BEЁЮDF.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЙигкЗНГЬx2+xЉ1=0ЕФЫЕЗЈжае§ШЗЕФЪЧЃЈ ЃЉ
A.ИУЗНГЬгаСНИіЯрЕШЕФЪЕЪ§Иљ
B.ИУЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧвЫќУЧЛЅЮЊЯрЗДЪ§
C.ИУЗНГЬгавЛИљЮЊ ![]()
D.ИУЗНГЬгавЛИљЧЁЮЊЛЦН№БШР§
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com