

���� ��1���ɵ��������е�Ķ���ɵ�BC=$\frac{1}{2}$OB�������t��ֵ�����PE=OA�����OE�ij��������E�����ꣻ
��2����PO��CD���ڵ�G������ƽ���ı��ε����ʿɵ�OG=PG���ٽ��������֤��AG=GE����֤���ı���ADECΪƽ���ı��Σ�
��3���ֵ�C��BO�Ϻ͵�C��BO���ӳ����������������C��BO��ʱ���ֵ�M��CE���Ϻ͵�N��DE���ϣ�����C��BO���ӳ�����ʱ���ֵ�M��DE���Ϻ͵�N��CE���ϣ��ٷֱ��������������ε��ж������ʿ����t��
��� �⣺��1����OB=6��C��OB���е㣬
��BC=$\frac{1}{2}$OB=3��
��2t=3����t=$\frac{3}{2}$��
��OE=OP+PE=OP+OA=$\frac{3}{2}$+3=$\frac{9}{2}$��
��E��$\frac{9}{2}$��0����
��2����ͼ1������CD��OP�ڵ�G��
���ı���PCODΪƽ���ı��Σ�
��CG=DG��OG=PG��
��AO=PE��
��AG=EG��
���ı���ADEC��ƽ���ı��Σ�
��3��������C��BO��ʱ����ͼ2��
��һ�����������M��CE����ʱ��
��MF��OC��
���EMF�ס�ECO��
��$\frac{MF}{CO}$=$\frac{EF}{EO}$����$\frac{2}{6-2t}$=$\frac{2}{3+t}$��
��t=1
�ڶ������������N��DE����ʱ��
��NF��PD��
���EFN�ס�EPD��
��$\frac{FN}{PD}$=$\frac{EF}{EP}$����$\frac{1}{6-2t}$=$\frac{2}{3}$��
��t=$\frac{9}{4}$��
������C��BO���ӳ�����ʱ����ͼ3��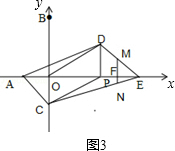
��һ�����������M��DE����ʱ��
��MF��PD��
���EMF�ס�EDP��
��$\frac{MF}{DP}$=$\frac{EF}{EP}$����$\frac{2}{2t-6}$=$\frac{2}{3}$��
��t=$\frac{9}{2}$��
�ڶ������������N��CE����ʱ��
��NF��OC��
���EFN�ס�EOC��
��$\frac{FN}{OC}$=$\frac{EF}{EO}$����$\frac{1}{2t-6}$=$\frac{2}{3+t}$��
��t=5��
��������������������tֵΪ1��$\frac{9}{4}$��$\frac{9}{2}$��5��
���� ������Ҫ�����ı��ε��ۺ�Ӧ�ã��漰������ꡢƽ���ı��ε����ʺ��ж������������ε��ж������ʵ�֪ʶ�㣮�ڣ�1�������t��ֵ����E������Ĺؼ����ڣ�2���������ı���PCODΪƽ���ı����ǽ���Ĺؼ����ڣ�3����ע�����÷������۵�˼�룬ȷ�������������εĶ�Ӧ���ǽ���Ĺؼ�������֪ʶ��϶࣬�ۺ��Խ�ǿ����һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ�������Ľֵ�������������������AD��BC�������ڽֵ�����������֮���AD������Ϊ45�㣬������BC������Ϊ57�㣬��֪��������ĸ߶�֮��Ϊ60�ף����ֵ���AB=50�ף�������BC�ĸ߶ȣ���sin57���0.83��cos57���0.54��tan57��1.5��
һ�������Ľֵ�������������������AD��BC�������ڽֵ�����������֮���AD������Ϊ45�㣬������BC������Ϊ57�㣬��֪��������ĸ߶�֮��Ϊ60�ף����ֵ���AB=50�ף�������BC�ĸ߶ȣ���sin57���0.83��cos57���0.54��tan57��1.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڲ�һ��Ʒ�۸����Ϸ�У����������Ȳ�֪������Ʒ�ļ۸�������Ҫ��������ͼ�����ſ�Ƭ�������������ţ�ʹʣ�µĿ�Ƭ����������һ����λ���������������µļ۸������Ʒ�ļ۸���50Ԫ������һ�ξ��ܲ��еĸ��ʣ�
�ڲ�һ��Ʒ�۸����Ϸ�У����������Ȳ�֪������Ʒ�ļ۸�������Ҫ��������ͼ�����ſ�Ƭ�������������ţ�ʹʣ�µĿ�Ƭ����������һ����λ���������������µļ۸������Ʒ�ļ۸���50Ԫ������һ�ξ��ܲ��еĸ��ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
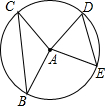 ��ͼ��ֱ��Ϊ5�ġ�A�У���BC��ED���Ե�Բ�ĽǷֱ��ǡ�BAC����EAD����֪DE=3����BAC+��EAD=180�㣬���A��BC�ľ��룮
��ͼ��ֱ��Ϊ5�ġ�A�У���BC��ED���Ե�Բ�ĽǷֱ��ǡ�BAC����EAD����֪DE=3����BAC+��EAD=180�㣬���A��BC�ľ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com