
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
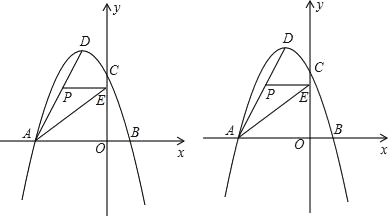
【答案】(1)抛物线解析式为:y=-![]() x2﹣2x+6,抛物线的顶点D(﹣2,8);(2)9;(3)P′(
x2﹣2x+6,抛物线的顶点D(﹣2,8);(2)9;(3)P′(![]() ,
,![]() ).
).
【解析】
1)由抛物线y=ax2+bx+c经过A、B、C三点,则代入求得a,b,c,进而得解析式与顶点D.
(2)由P在AD上,则可求AD解析式表示P点.由S△APE=![]() PEyP,所以S可表示,进而由函数最值性质易得S最值.
PEyP,所以S可表示,进而由函数最值性质易得S最值.
(3)求出点P,过点P′作P′M⊥y轴于点M,再根据相关条件解答即可.
解:(1)∵抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,6)三点,
∴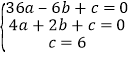 ,解得:
,解得: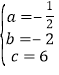 ,
,
∴抛物线解析式为:y=![]() x2﹣2x+6,
x2﹣2x+6,
∵![]() ,
,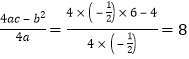 ,
,
∴抛物线的顶点D(﹣2,8);
(2)∵A(﹣6,0),D(﹣2,8),
∴设AD的解析式y=2x+12,
∵点P在AD上,
∴P(x,2x+12),
∴S△APE=![]() PEyP=
PEyP=![]() ×(﹣x)(2x+12)=﹣x2﹣6x,
×(﹣x)(2x+12)=﹣x2﹣6x,
当x=-3时,S最大=9;
(3)P′(![]() ,
,![]() ).
).
点P在AD上,
∴当﹣3时,y=2×(﹣3)+12=6,
∴点P(﹣3,6),
∴PF=6,PE=3,
过点P′作P′M⊥y轴于点M,
∵△PEF沿EF翻折得△P′EF,
∴∠PFE=∠P′FE,PF=P′F=6,PE=P′E=3,
∵PF∥y轴,
∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,
∴∠FEN=∠P′FE,
∴EN=FN,
设EN=a,则FN=a,P′N=6﹣a,
在Rt△P′EN中,P′N2+P′E2=EN2,即(6﹣a)2+32=a2,解得:a=![]() ,
,
∵S△P′EN=![]() P′NP′E=
P′NP′E=![]() ENP′M,
ENP′M,
∴P′M=![]() ,
,
在Rt△EMP′中,EM=![]() ,
,
∴OM=EO﹣EM=6﹣![]() =
=![]() ,
,
∴P′(![]() ,
,![]() ).
).


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】(12分)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.

(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
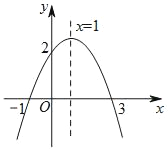
【题目】二次函数y=ax2+bx+c(a≠0,a,b,c为常数)图象如图所示,根据图象解答问题.
(1)写出过程ax2+bx+c=0的两个根.
(2)写出不等式ax2+bx+c>0的解集.
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
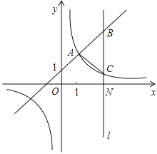
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B'作B'P∥BC,交AE于点P,连接BP.已知BC=3,CB'=1,下列结论:①AB=5;②sin∠ABP=![]() ;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( )
;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( )
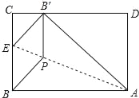
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=x2+bx+![]() 与 y轴交于点 B,将该抛物线平移,使其经过点 A(-
与 y轴交于点 B,将该抛物线平移,使其经过点 A(-![]() ,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
A. OB≤OC B. OB<OC C. OB≥OC D. OB>OC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com