
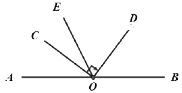
【题目】如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
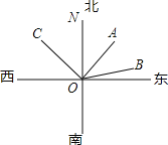
(1)求∠BOC的度数;
(2)求∠AOB的度数.
【答案】(1)120°20′;(2)32°50′.
【解析】
(1)根据方向角的表示方法,可得∠NOA,∠NOB,∠NOC的度数,根据∠BOC=∠NOB+∠NOC可得答案;
(2)根据∠AOB=∠NOB-∠NOA,可得答案.
解:(1)∵甲船位于港口的北偏东43°45′方向,
乙船位于港口的北偏东76°35′方向,
丙船位于港口的北偏西43°45′方向,
∴∠NOA=43°45′,∠NOB=76°35′,∠NOC=43°45′,
∴∠BOC=∠NOB+∠NOC=76°35′+43°45′=120°20′;
(2)∵∠NOA=43°45′,∠NOB=76°35′,
∴∠AOB=∠NOB-∠NOA=76°35′-43°45′=32°50′.


科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,已知抛物线C1:y1=﹣x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,抛物线C1与x轴交于点A、C,与y轴交于点B.
(1)求抛物线C1的表达式.
(2)若F(t,0)(﹣3<t<0)是x轴上的一点,过点F作x轴的垂线交抛物线与点P,交直线AB于点E,过点P作PD⊥AB于点D.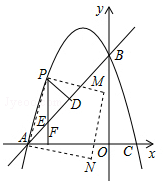
①是否存在点F,使PE+PD的值最大,若存在,请求出t的值;若不存在,请说明理由.
②连接PA,以AP为边作图示一侧的正方形APMN,随着点F的运动,正方形的大小、位置也随之改变.当正方形APMN中的边MN与y轴有且仅有一个交点时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行春季运动会,需要在初三年级选取1或2名同学作为志愿者,初三(5)班的小熊、小乐和初三(6)班的小矛、小管4名同学报名参加.
(1)若从这4名同学中随机选取1名志愿者,则被选中的这名同学恰好是初三(5)班同学的概率是;
(2)若从这4名同学中随机选取2名志愿者,请用列举法(画树状图或列表)求这2名同学恰好都是初三(6)班同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)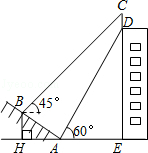
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() 1.414,
1.414, ![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
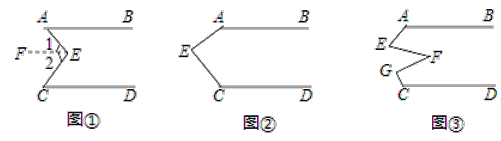
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、O、B在一条直线上,将射线OC绕O点顺时针方向旋转90°后,得到射线OD,在旋转过程中,射线OC始终在直线AB上方,且OE平分∠AOD.约定,无论∠AOD大小如何,OE都看作是由OA、OD两边形成的最小角的平分线.
(1)如图,当∠AOC=30°时,∠BOD=_________°;
(2)若射线OF平分∠BOC,求∠EOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com