
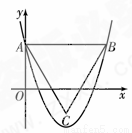
如图,已知△OAB的顶点A(﹣6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
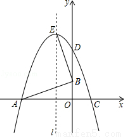
(1)写出C,D两点的坐标;
(2)求过A,D,C三点的抛物线的解析式,并求此抛物线顶点E的坐标;
(3)证明AB⊥BE
(1)C(2,0),D(0,6);
(2)y=-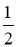 x2﹣2x+6;顶点E的坐标为(﹣2,8).
x2﹣2x+6;顶点E的坐标为(﹣2,8).
(3)证明见解析.
【解析】
试题分析:(1)由旋转的性质可得OC=OB,OD=OA,由已知条件即可得点C、D的坐标;
(2)由于抛物线过点A(﹣6,0),C(2,0),所以设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),再将D(0,6)代入,求出a的值,得出抛物线的解析式,然后利用配方法求出顶点E的坐标;
(3)已知A、B、E三点的坐标,运用勾股定理计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
试题解析:(1)∵将△OAB绕点O按顺时针旋转90°,得到△ODC,∴△ODC≌△OAB.
∴OC=OB=2,OD=OA=6.∴C(2,0),D(0,6).
(2)∵抛物线过点A(﹣6,0),C(2,0),
∴可设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),
∵D(0,6)在抛物线上,∴6=﹣12a,解得a=-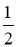 .
.
∴抛物线的解析式为y=-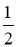 (x+6)(x﹣2),即y=-
(x+6)(x﹣2),即y=-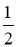 x2﹣2x+6.
x2﹣2x+6.
∵y=-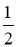 x2﹣2x+6=-
x2﹣2x+6=-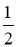 (x+2)2+8,∴顶点E的坐标为(﹣2,8).
(x+2)2+8,∴顶点E的坐标为(﹣2,8).
(3)连接AE,
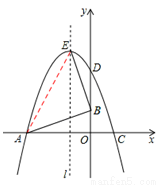
∵A(﹣6,0),B(0,2),E(﹣2,8),
∴AB2=62+22=40,
BE2=(﹣2﹣0)2+(8﹣2)2=40,
AE2=(﹣2+6)2+(8﹣0)2=80.
∴AB2+BE2=AE2.
∴△ABE是直角三角形.
∴AB⊥BE.
考点:1、旋转的性质;2、待定系数法求函数解析式;3、勾股定理的逆定理.


科目:初中数学 来源:2014-2015学年天津市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,点A是抛物线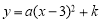 与y轴的交点,点B是这条抛物线上另一点.且AB//x轴,则以AB为边的等边三角形ABC的周长为 .
与y轴的交点,点B是这条抛物线上另一点.且AB//x轴,则以AB为边的等边三角形ABC的周长为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年上海市闸北九年级期末考试数学试卷(解析版) 题型:选择题
已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
(A)BD︰AB = CE︰AC; (B)DE︰BC = AB︰AD;
(C)AB︰AC = AD︰AE; (D)AD︰DB = AE︰EC.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七校九年级上学期联考数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=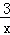 (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
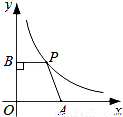
A.逐渐增大 B. 不变C. 逐渐减小 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七校九年级上学期联考数学试卷(解析版) 题型:选择题
根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
A.3<x<3.23 B. 3.23<x<3.24 C. 3.24<x<3.25 D. 3.25<x<3.26
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古巴彦淖尔乌拉特前旗四中九年级上学期期末考试数学试卷(解析版) 题型:填空题
要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场)计划安排15场比赛,应邀请 个球队参加比赛.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古巴彦淖尔乌拉特前旗四中九年级上学期期末考试数学试卷(解析版) 题型:填空题
弦AB把圆周分成1:3的两部分,点C是圆上不同于A 、B的一点,那么∠ACB的度数为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市开发区九年级上学期第三次质量检测数学试卷(解析版) 题型:解答题
(本题满分8分)
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
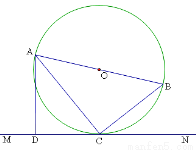
(1)猜想直线MN与⊙O的位置关系,并说明理由,
(2)若CD=6,cos∠ACD=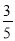 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com