
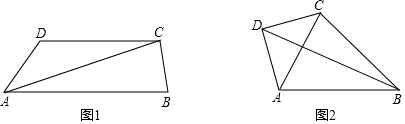
·ÖĪö £Ø1£©·Ö±š¼ĘĖćĮ½Čż½ĒŠĪø÷½ĒµÄ¶ČŹż£¬²¢¼ĘĖćĘäĘ½·½ŗĶæÉŅŌ×÷ÅŠ¶Ļ£»
£Ø2£©Óɹ“¹ÉČż½ĒŠĪµÄ¶ØŅåĒŅx£¼y£¼zµĆ£ŗz2=x2+y2£¬±äŠĪŗóµĆ£ŗ£Ø180-17m£©2=289m2-720m£¬Ēó³ömµÄÖµ£¬²¢¼ĘĖć×ī“ó½ĒzµÄÖµ¼“æÉ£»
£Ø3£©ĻČĖµĆ÷”÷ADCĪŖ¹“¹ÉČż½ĒŠĪ²»³ÉĮ¢£»Ōņµ±”÷ACBŅ»¶ØŹĒ¹“¹ÉČż½ĒŠĪ£¬×÷øØÖśĻߣ¬¹¹½ØÖ±½ĒČż½ĒŠĪ£¬Č·¶Ø”ĻACBĪŖ×ī“ó½Ē£¬Éč”ĻABC=x”ć£¬”ĻCAB=y”ć£¬Ōņ”ĻACB=30+x£¬øł¾Ż¹“¹ÉČż½ĒŠĪµÄ¶ØŅåŗĶČż½ĒŠĪÄŚ½ĒŗĶĮŠ·½³Ģ×é£ŗŌņ$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=£Ø30+x£©^{2}}\\{2x+y+30=180}\end{array}\right.$£¬½ā³ö£¬Č·¶Ø”÷BECŗĶ”÷ADCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬ÉčAE=a£¬ŌņAC=2a£¬CE=$\sqrt{3}$a£¬·Ö±š±ķŹ¾AC”¢ABŗĶBDµÄ³¤£¬ÕŅ¹ŲĻµ¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©”ß”ĻCAB£ŗ”ĻCAD£ŗ”ĻD=1£ŗ3£ŗ6£¬
”ą”ĻCAD=3”ĻCAB£¬”ĻD=6”ĻCAB£¬
”ą”ĻBAD=4”ĻCAB£¬
”ßAB”ĪCD£¬
”ą”ĻBAD+”ĻD=180”ć£¬”ĻCAB=”ĻACD£¬
”ą4”ĻCAB+6”ĻCAB=180”ć£¬
”ą”ĻCAB=18”ć£¬
”ą”ĻCAD=54”ć£¬”ĻACD=18”ć£¬”ĻD=108”ć£¬
”ß182+542”Ł1082£¬
”ą”÷ACD²»ŹĒ¹“¹ÉČż½ĒŠĪ£»
”ß”ĻB=80”ć£¬
”ą”ĻACB=180”ć-18”ć-80”ć=82”ć£¬
”ß182+802=822£¬
”ą”÷ABCŹĒ¹“¹ÉČż½ĒŠĪ£»
£Ø2£©ÓÉĢāŅāµĆ£ŗz2=x2+y2£¬
”ßx+y=17m£¬xy=360m£¬
”ąz2=£Øx+y£©2-2xy=289m2-720m£¬
”ßx+y+z=180”ć£¬
”ą£Ø180-17m£©2=289m2-720m£¬
½āµĆ£ŗm=6£¬
”ąz=180-17m=78”ć£¬
”ąøĆČż½ĒŠĪ×ī“óÄŚ½ĒµÄ¶ČŹżĪŖ78”ć£»
£Ø3£©²ĀĻė£ŗŅŌAB”¢AC”¢BDĪŖČż±ßĪ§³ÉµÄČż½ĒŠĪÖ±½ĒČż½ĒŠĪ£¬
ĄķÓÉŹĒ£ŗČēĶ¼2£¬·ÖĮ½ÖÖĒéæö£ŗ
¢Łµ±”÷ADCĪŖ¹“¹ÉČż½ĒŠĪŹ±£¬Éč”ĻDAC=x”ć£¬”ĻACD=y”ć£¬
”ß”ĻADC=90”ć£¬
”ąx2+y2=902¢Ł£¬
”ßx+y=90£¬
”ą£Øx+y£©2=902£¬
¼“x2+2xy+y2=902¢Ś£¬
°Ń¢Ł“śČė¢ŚµĆ£ŗ2xy=0£¬
”ßx”Ł0£¬y”Ł0£¬
”ą2xy”Ł0£¬
”ą”÷ADCĪŖ¹“¹ÉČż½ĒŠĪ²»³ÉĮ¢£»
¢Śµ±”÷ACBŹĒ¹“¹ÉČż½ĒŠĪŹ±£¬ŌŚABÉĻČ”Ņ»µćE£¬Į¬½ÓCE£¬Ź¹CE=BE£¬Ōņ”ĻABC=”ĻBCE£¬
”ß”ĻABC£¾40”ć£¬”ĻACB-”ĻABC=30”ć£¬
”ą”ĻABC£¾70”ć£¬
”ą”ĻCAB£¼70”ć£¬
”ą”ĻACBĪŖ×ī“ó½Ē£¬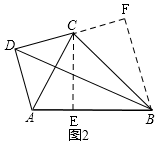
Éč”ĻABC=x”ć£¬”ĻCAB=y”ć£¬Ōņ”ĻACB=30+x£¬
Ōņ$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=£Ø30+x£©^{2}}\\{2x+y+30=180}\end{array}\right.$£¬
Ōņ$\left\{\begin{array}{l}{y=150-2x¢Ł}\\{{x}^{2}+{y}^{2}=£Ø30+x£©^{2}¢Ś}\end{array}\right.$£¬
°Ń¢Ł“śČė¢ŚµĆ£ŗ£Ø150-2x£©2=900+60x£¬
x2-165x+5400=0£¬
£Øx-120£©£Øx-45£©=0£¬
x1=120”ć£¬x2=45”ć£¬
µ±x=120Ź±£¬y=150-2”Į120=-90£¼0£¬²»·ūŗĻĢāŅā£¬ÉįČ„£¬
”ą”ĻABC=”ĻBCE=45”ć£¬
”ĻCAB=y=150-2x=60”ć£¬
ÉčAE=a£¬ŌņAC=2a£¬CE=$\sqrt{3}$a£¬
”ąBE=$\sqrt{3}$a£¬BC=$\sqrt{6}$a£¬
”ßBC=$\sqrt{3}$AD£¬
”ą$\sqrt{6}$a=$\sqrt{3}$AD£¬
”ąAD=$\sqrt{2}$a£¬
ŌŚRt”÷ADCÖŠ£¬DC=$\sqrt{£Ø2a£©^{2}-£Ø\sqrt{2}a£©^{2}}$=$\sqrt{2}$a£¬
”ą”÷ADCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻDCA=45”ć£¬
¹żB×÷BF”ĶDC£¬½»DCµÄŃÓ³¤ĻßÓŚF£¬
”ą”ĻBCF=180”ć-45”ć-30”ć-45”ć=60”ć£¬
”ą”ĻCBF=30”ć£¬
”ąCF=$\frac{1}{2}$BC=$\frac{\sqrt{6}}{2}$a£¬BF=$\frac{3\sqrt{2}}{2}$a£¬
Rt”÷DFBÖŠ£¬BD2=DF2+BF2=£Ø$\sqrt{2}$a+$\frac{\sqrt{6}}{2}$a£©2+£Ø$\frac{3\sqrt{2}}{2}$a£©2=8a2+2$\sqrt{3}$a2£¬
”ßAB2+AC2=£Øa+$\sqrt{3}$a£©2+£Ø2a£©2=8a2+2$\sqrt{3}$a2£¬
”ąAB2+AC2=BD2£¬
”ąŅŌAB”¢AC”¢BDĪŖČż±ßĪ§³ÉµÄČż½ĒŠĪÖ±½ĒČż½ĒŠĪ£®
µćĘĄ “ĖĢāÖ÷ŅŖæ¼²éĮĖŠĀ¶ØŅåŅŌ¼°¶ąŌŖ·½³Ģ×é½ā·ØŅŌ¼°¹“¹É¶ØĄķŗĶČń½ĒČż½ĒŗÆŹż¹ŲĻµ£¬µŚ3ĪŹÓŠÄŃ¶Č£¬ĄūÓĆ¹“¹É¶ØĄķµĆ³öAB”¢AC”¢BDµÄ³¤ŹĒ½āĢā¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ČĪŅāĖıߊĪ | B£® | Ę½ŠŠĖıߊĪ | ||
| C£® | ¶Ō½ĒĻßĻąµČµÄĖıߊĪ | D£® | ¶Ō½ĒĻß“¹Ö±µÄĖıߊĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
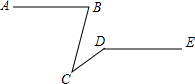 ČēĶ¼£¬ŅŃÖŖAB”ĪDE£¬”ĻABC=75”ć£¬”ĻCDE=145”ć£¬Ōņ”ĻBCDµÄÖµĪŖ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖAB”ĪDE£¬”ĻABC=75”ć£¬”ĻCDE=145”ć£¬Ōņ”ĻBCDµÄÖµĪŖ£Ø””””£©| A£® | 20”ć | B£® | 30”ć | C£® | 40”ć | D£® | 70”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼ŹĒŅ»øö¼øŗĪĢåµÄČżŹÓĶ¼£¬ø©ŹÓĶ¼ŹĒĮāŠĪ£¬øł¾ŻĶ¼ÖŠŹż¾Ż£Øµ„Ī»£ŗdm£©£¬æÉĒóµĆĖüµÄĢå»ż£Øµ„Ī»£ŗdm3£©ŹĒ£Ø””””£©
ČēĶ¼ŹĒŅ»øö¼øŗĪĢåµÄČżŹÓĶ¼£¬ø©ŹÓĶ¼ŹĒĮāŠĪ£¬øł¾ŻĶ¼ÖŠŹż¾Ż£Øµ„Ī»£ŗdm£©£¬æÉĒóµĆĖüµÄĢå»ż£Øµ„Ī»£ŗdm3£©ŹĒ£Ø””””£©| A£® | 80 | B£® | 240 | C£® | 250 | D£® | 480 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
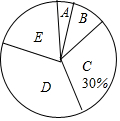 ĪŖĮĖĮĖ½āijŠ£¾ÅÄź¼¶£Ø1£©°ąŃ§ÉśµÄĢåÓż²āŹŌĒéæö£¬¶ŌČ«°ąŃ§ÉśµÄĢåÓż³É¼Ø½ųŠŠĮĖĶ³¼Ę£¬²¢»ęÖĘ³öŅŌĻĀ²»ĶźÕūµÄʵŹż·Ö²¼±ķŗĶÉČŠĪĶ³¼ĘĶ¼
ĪŖĮĖĮĖ½āijŠ£¾ÅÄź¼¶£Ø1£©°ąŃ§ÉśµÄĢåÓż²āŹŌĒéæö£¬¶ŌČ«°ąŃ§ÉśµÄĢåÓż³É¼Ø½ųŠŠĮĖĶ³¼Ę£¬²¢»ęÖĘ³öŅŌĻĀ²»ĶźÕūµÄʵŹż·Ö²¼±ķŗĶÉČŠĪĶ³¼ĘĶ¼| ·Ö×é | ·ÖŹż¶Ī£Ø·Ö£© | ʵŹż |
| A | 36”Üx£¼41 | 2 |
| B | 41”Üx£¼46 | 5 |
| C | 46”Üx£¼51 | 15 |
| D | 51”Üx£¼56 | m |
| E | 56”Üx£¼61 | 10 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com