
【题目】如图,在△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线.
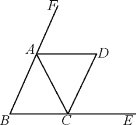
(1)求证:∠ACD=∠ADC;
(2)若∠B=60°,求证:四边形ABCD是菱形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据角平分线的性质和等腰三角形的性质得出∠FAD=∠B,进而得到AD∥BC,再利用∠D=∠DCE,即可证明∠ACD=∠ADC;
(2)首先证明△ABC和△ADC是等边三角形,进而得到AD=CB=AB=CD,可判定四边形ABCD是菱形.
证明:(1)∵AB=AC,
∴∠B=∠ACB,
在△ABC中,
∠FAC=∠B+∠ACB=2∠B.
∵AD平分∠FAC,
∴∠FAC=2∠FAD=2∠CAD,
∴∠FAD=∠B,
∴AD∥BC.
∴∠D=∠DCE.
∵CD平分∠ACE,
∴∠ACD=∠DCE.
∴∠ACD=∠ADC
(2)∵∠B=60°,
∴∠ACB=∠CAD=60°,
∵AB=AC,∠ACD=∠ADC,
∴△ABC和△ACD都是等边三角形.
∴AB=BC=AC=CD=AD,
∴四边形ABCD是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=![]() +1,求BC的长.
+1,求BC的长.
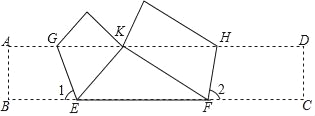
查看答案和解析>>
科目:初中数学 来源: 题型:
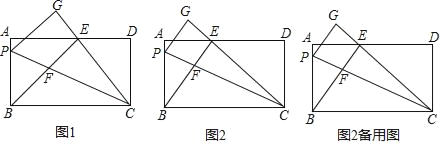
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
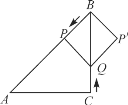
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒![]() cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
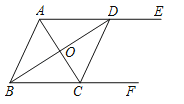
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
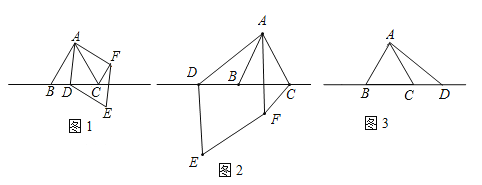
【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=![]() AB,求AG的长.
AB,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
(1)已知如图1,若AB∥CD,P为平行线内的一点请你判断∠B+∠P+∠D= 度,并说明理由.
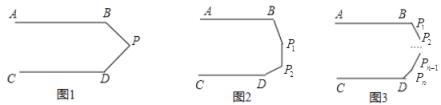
(2)如图2,若AB∥CD ,P1、P2为平行线内的两个点,请求出∠B+∠P1+∠P2+∠D= 度(不需要说明理由)
(3)如图3,如此类推若AB∥CD,P1、、P2、P3、P4、……Pn为平行线内的n个点,请求出∠B+∠P1+∠P2+∠P3+…….+∠Pn-1+∠Pn+∠D= 度(不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有两条边相等的三角形叫做等腰三角形。类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请你写出一个等对边四边形的名称;
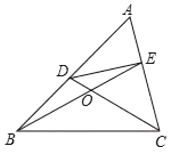
(2)如图,在△ABC中,点D、E分别在AB、AC上,设CD、BE相交于点O,若∠A=50°,![]() .请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
.请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
(3)在![]() 中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且
中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且![]() .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com