
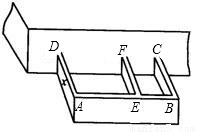
 (x-3)2+
(x-3)2+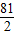


科目:初中数学 来源: 题型:
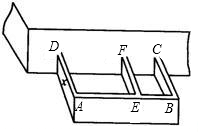 墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度)
墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度)查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江慈溪育才中学九年级第一学期第二次月考数学试卷(解析版) 题型:解答题
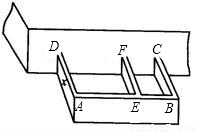
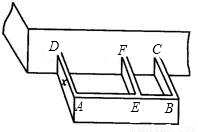
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度).
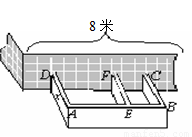
(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
查看答案和解析>>
科目:初中数学 来源:《第26章 二次函数》2010年复习题(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》常考题集(18):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com