
 如图,这是一个可以自由转动的三色转盘,求出下列事件的概率:
如图,这是一个可以自由转动的三色转盘,求出下列事件的概率:分析 用所在扇形圆心角的度数除以周角的度数即可求得转出该色的概率.
解答 解:∵白色扇形的圆心角为45°,红色扇形的圆心角为90°,
∴黄色扇形的圆心角为360°-90°-45°=225°,
∴(1)P(转出红色)=$\frac{90}{360}$=$\frac{1}{4}$;
(2)P(转出白色)=$\frac{45}{360}$=$\frac{1}{8}$;
(3)P(转出黄色)=$\frac{225}{360}$=$\frac{5}{8}$,
故答案为:$\frac{1}{4}$,$\frac{1}{8}$,$\frac{5}{8}$.
点评 本题考查了几何概率的知识,解题的关键是能够了解概率的求法为扇形的圆心角的度数与周角的度数的比,难度不大.


科目:初中数学 来源: 题型:选择题
| A. | 8的立方根是±2 | B. | $-\frac{1}{2}$是$-\frac{1}{6}$的立方根 | ||
| C. | 负数没有立方根 | D. | $\root{3}{-64}$=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
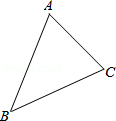 画图并讨论:已知△ABC,如图所示,要求画一个三角形,使它与△ABC有一个公共的顶点C,并且与△ABC全等.
画图并讨论:已知△ABC,如图所示,要求画一个三角形,使它与△ABC有一个公共的顶点C,并且与△ABC全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
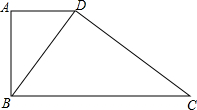 直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )
直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )| A. | 12米 | B. | 13米 | C. | 5米 | D. | 6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
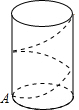 一只昆虫从A点绕着圆柱沿着最短路线螺旋前进
一只昆虫从A点绕着圆柱沿着最短路线螺旋前进查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com