
����Ŀ������С����������ij��˾��Ʊ1000�ɣ�ÿ��14.80Ԫ����Ϊ�ڶ�������һ��������ÿ�ոù�Ʊ�ǵ����.
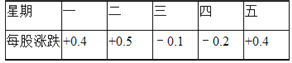
��1������������ʱ��ÿ���Ƕ���Ԫ��
��2�������������ÿ�ɶ���Ԫ����ͼ���ÿ�ɶ���Ԫ��
��3����֪С�������Ʊʱ���˳ɽ���0.15%�������ѣ�����ʱ���˳ɽ���0.15%�������Ѻͳɽ���0.1%�Ľ���˰�����С��������������ǰ��ȫ����Ʊ��������ô�������������Σ�
���𰸡���1��ÿ����15.6Ԫ��
��2�������������ÿ��15.8Ԫ����ͼ���ÿ��15.2Ԫ��
��3��С����938.3Ԫ��
�������������������1����ÿ��ԭ�ۼ���ÿ��ÿ���ǵ������Ǹ���ÿ�ɵ�Ǯ����
��2������ͳ�Ʊ����ṩ��ÿ���ǵ������ݣ����ǵ������ֵ���ϳɱ��۾��DZ��������ÿ�ɵ�Ǯ����ͬ�����õ��������ֵ���ϳɱ��۾��DZ�������ͼ�ÿ�ɵ�Ǯ����
��3��������ÿ���ǵ�Ǯ����1000���ٷֱ��ȥ�����Ʊʱ���������ѡ�����ʱ���������ѡ�����˰�������������森
����������⣺��1��14.8+0.4+0.5��0.1=15.6��Ԫ����
��ÿ����15.6Ԫ��
��2��14.8+0.4+0.5��0.1��0.2+0.4=15.8��Ԫ����
14.8+0.4=15.2��Ԫ����
�ʱ����������ÿ��15.8Ԫ����ͼ���ÿ��15.2Ԫ��
��3������1000�ŵķ����ǣ�1000��14.8=14800��Ԫ����
������ȫ����Ʊ����ʱ����Ǯ��Ϊ��1000��15.80=15800��Ԫ��
15800��14800��14800��0.15%��15800����0.15%+0.1%��
=1000��22.2��39.5
=938.3��Ԫ����
����С����938.3Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������뷨��0.0257��ȷ��0.001����ǣ� ��
A.0.03
B.0.026
C.0.025
D.0.0257
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.ƽ���ı��ζԽ������B.���εĶԽ����ഹֱ
C.���ε��ĸ��Ƕ����D.�����εĶԽ�����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺������������Ʒ���Ľ������۱��ҵĽ������۸�20Ԫ����֪20������Ʒ�Ľ����ܼ���25������Ʒ�Ľ����ܼ���ͬ��
��1����ס���ÿ����Ʒ�Ľ������ۣ�
��2�����ס���������Ʒ������100����Ҫ��������Ʒ�Ľ����ܼ۲�����9000Ԫ��ͬʱ����Ʒ���������10%��ļ۸����ۣ�����Ʒ���������25%��ļ۸����ۣ�������Ʒȫ�������������ܶ����10480Ԫ�������ļ��ֽ���������
��3����������2���£����Ҳ��ٿ����������أ�������������Ʒȫ�����꣬���ַ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ���ȷ���ǣ�������
A.3ax2��6ax��3 ��ax2��2ax��B.x2+y2������x+y������x��y��
C.a2+2ab��4b2����a+2b��2D.ax2��2ax+a��a ��x��1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
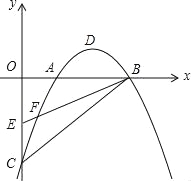
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0����1��������������BE������һ��F������BC��
��1����������ߵĽ���ʽ�������䷽���ѽ���ʽ��Ϊy=a��x��h��2+k����ʽ��
��2������H��1��y����BC�ϣ�����FH�����FHB�������
��3��һ����M�ӵ�D��������ÿ��1����λ���ٶ�ƽ������y�᷽�������˶�������OM��BM�����˶�ʱ��Ϊt�루t��0�����ڵ�M���˶������У���tΪ��ֵʱ����OMB=90�㣿
��4����x���Ϸ����������ϣ��Ƿ���ڵ�P��ʹ�á�PBF��BAƽ�֣������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O����BOC��80�㣬OE�ǡ�BOC�Ľ�ƽ���ߣ�OF��OE�ķ����ӳ��ߣ�
��1�����2����3�Ķ�����
��2��˵��OFƽ�֡�AOD�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˽⣬�ܵ�̨�硰��������Ӱ�죬������������ũ�����������Լ��35800Ķ������35800�ÿ�ѧ�������ɱ�ʾΪ�� ��
A.0.358��105
B.3.58��104
C.35.8��103
D.358��102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�Сӱ��С÷���ܵ�·��s(��)������ʱ��t(��)֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD������˵����ȷ���ǣ� ��
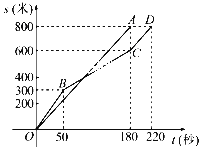
A. Сӱ���ٶ���ʱ������������
B. С÷���ٶ���ʱ����������С
C. �����ܺ�180��ʱ����������
D. �����ܺ�50��ʱ��С÷��Сӱ��ǰ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com