
分析 先根据a判断出抛物线的开口向下,故有最大小值,对称轴x=0,
(1)根据当2<x<3时,在对称轴的右侧,y随着x的增大而减小,代入求得最大值与最小值求得答案即可.
(2)根据当-2<x<3时,在对称轴的两侧,代入求得最小值求得答案即可.
(3)代入求得x的值,根据二次函数的性质求得即可.
解答 解:∵二次函数y=-x2中a=-1<0,
∴抛物线开口向下,有最大小值为0,抛物线的对称轴为y轴,
(1)当2<x<3时,在对称轴的右侧,y随着x的增大而减小,
当x=2时,y=-4,
当x=3时,y=-9
∴-9<y<-4;
(2)当-2<x<3时,在对称轴的两侧,
当x=-2时,y=-4,
当x=3时,y=-9
∴-9<x≤0;
(3)当-4<y<-1时,
当y=-4时,x=±2,
当y=-1时,x=±1,
∴-2<x<-1或1<x<2.
故答案为-9<x<4;-9<x≤0;2<x<-1或1<x<2.
点评 本题考查的是二次函数的性质,在解答此题时要先确定出抛物线的对称轴及最大值,再根据x和y的取值范围进行解答.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
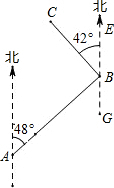 如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长12千米,另一条公路BC长是5千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )
如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长12千米,另一条公路BC长是5千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )| A. | 5千米 | B. | 12千米 | C. | 13千米 | D. | 17千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
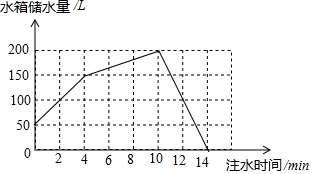 容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.
容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
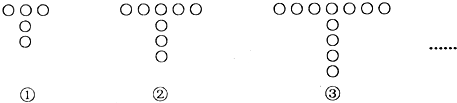
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com