Question

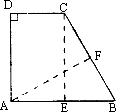
某工程师设计一零件图纸，零件的截面如图，是一直角梯形，其中CD∥AB，∠A＝∠D＝90°，AD＝12，CD＝8，AB＝13，试求点A到BC边的距离．

Answer 1

答案：
解析：

解：分别过A、C作AF⊥BC，CE⊥AB，则△CBE是直角三角形，由于∠DAB＝∠D＝90°，所以四边形AECD是长方形，因此CE＝AD＝12，AE＝CD，所以BE＝AB－AE＝AB－CD＝5，在Rt△CBE中，CE＝12，BE＝5，所以BC＝13＝AB，由作图可知∠AFB＝∠BEC＝90°，∠B＝∠B，BC＝AB，所以△ABF≌△CBE，因此AF＝CE＝12，所以A点到BC的距离是12． 　　分析：由于截面是一个直角梯形，所以可以把直角梯形转化为直角三角形和长方形，由已知条件可证△ABF≌△CBE，因此AF＝CE＝12．

提示：

对于点到线的距离通常可以转化为其他相等的线段，也可以将它转化到特殊的图形中去解决．