
| A. | x2-$\sqrt{3}$x+$\frac{1}{2}$=0 | B. | x2+$\sqrt{3}$x+$\frac{1}{2}$=0 | C. | x2-$\sqrt{3}$x+1=0 | D. | x2+$\sqrt{3}$x-$\frac{1}{2}$=0 |
分析 将$\frac{1+\sqrt{3}}{2}$和$\frac{-1+\sqrt{3}}{2}$相加、相乘,再结合根与系数的关系即可找出以$\frac{1+\sqrt{3}}{2}$和$\frac{-1+\sqrt{3}}{2}$为根的一个一元二次方程.
解答 解:∵$\frac{1+\sqrt{3}}{2}$+$\frac{-1+\sqrt{3}}{2}$=$\sqrt{3}$,$\frac{1+\sqrt{3}}{2}$×$\frac{-1+\sqrt{3}}{2}$=$\frac{1}{2}$,
∴以$\frac{1+\sqrt{3}}{2}$和$\frac{-1+\sqrt{3}}{2}$为根的一个一元二次方程是x2-$\sqrt{3}$x+$\frac{1}{2}$=0.
故选A.
点评 本题考查了根与系数的关系,牢记两根之和等于-$\frac{b}{a}$、两根之积等于$\frac{c}{a}$是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:| 课外作业时间 (分组) | 人数 (频数) |
| 30~45 | 5 |
| 45~60 | 12 |
| 60~75 | a |
| 75~90 | 10 |
| 90~105 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
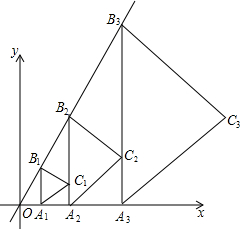 如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).
如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
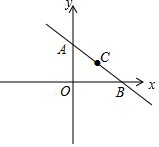 如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).
如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
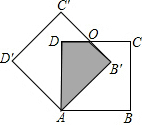 如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.
如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com