
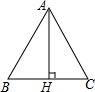
 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
分析 利用等边三角形的性质以及解直角三角形的知识求出BC的长,即可求出△ABC的面积.
解答 解:∵AB=AC=BC,
∴BH=CH=$\frac{1}{2}$CB=$\frac{1}{2}$AB,∠BAH=30°,
∵AH=$\sqrt{3}$,
∴cos30°=$\frac{AH}{AB}$,
∴AB=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2cm,
∴BC=2cm,
∴△ABC的面积为:$\frac{1}{2}$•CB•AH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$(cm2).
故选A.
点评 本题考查了等边三角形的性质以及解直角三角形,解决问题的关键是利用解直角三角形求出BC的长.


科目:初中数学 来源: 题型:填空题
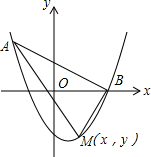 如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.
如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
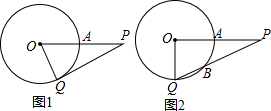 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
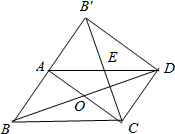 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
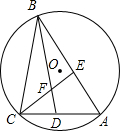 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com