
ЁОЬтФПЁПШчЭМЃЌЮЊМгПь5GЭјТчНЈЩшЃЌФГЭЈаХЙЋЫОдквЛИіЦТЖШiЃН1ЃК2.4ЕФЩНЦТABЩЯНЈСЫвЛзљаХКХЫўCDЃЌаХКХЫўЕзЖЫCЕНЩННХAЕФОрРыACЃН13УзЃЌдкОрЩННХAЫЎЦНОрРы18УзЕФEДІЃЌгавЛИпЖШЮЊ10УзЕФНЈжўЮяEFЃЌдкНЈжўЮяЖЅЖЫFДІВтЕУаХКХЫўЖЅЖЫDЕФбіНЧЮЊ37ЁуЃЈаХКХЫўМАЩНЦТЕФЦЪУцКЭНЈжўЮяЕФЦЪУцдкЭЌвЛЦНУцЩЯЃЉЃЌдђаХКХЫўCDЕФИпЖШдМЪЧЃЈЁЁЁЁЃЉЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ
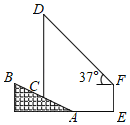
A.22.5УзB.27.5УзC.32.5УзD.45.0Уз
ЁОД№АИЁПB
ЁОНтЮіЁП
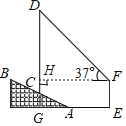
Й§ЕуFзїFHЁЭDCгкЕуHЃЌбгГЄDCНЛEAгкЕуGЃЌПЩЕУЫФБпаЮEFHGЪЧОиаЮЃЌИљОнABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌПЩЕУCGЃН5ЃЌAGЃН12ЃЌCHЃНGHЉCGЃН10Љ5ЃН5ЃЌдйИљОнШёНЧШ§НЧКЏЪ§МДПЩЧѓГіаХКХЫўCDЕФИпЖШЃЎ
НтЃКШчЭМЃЌЙ§ЕуFзїFHЁЭDCгкЕуHЃЌ
бгГЄDCНЛEAгкЕуGЃЌ
дђЫФБпаЮEFHGЪЧОиаЮЃЌ
ЁрFHЃНGEЃЌCGЃНEFЃЌ
ЁпABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌ
ЁрCGЃН5ЃЌAGЃН12ЃЌ
ЁрCHЃНGHЉCGЃН10Љ5ЃН5ЃЌ
ЁрGEЃНAG+AEЃН12+18ЃН30ЃЌ
ЁрдкRtЁїDCFжаЃЌЁЯDFCЃН37ЁуЃЌFHЃНGEЃН30ЃЌ
ЁрDHЃНFHtan37ЁуЁж30ЁС0.75Ёж22.5ЃЌ
ЁрCDЃНDH+CHЁж22.5+5Ёж27.5ЃЈУзЃЉЃЎ
ЫљвдаХКХЫўCDЕФИпЖШдМЪЧ27.5УзЃЎ
ЙЪбЁЃКBЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ
ЃЈ1ЃЉЗНЗЈЬхбщЃК
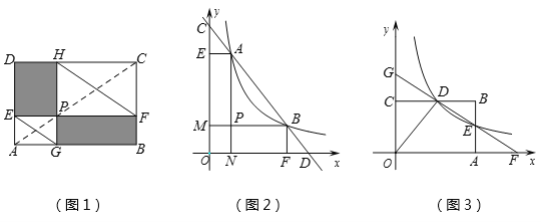
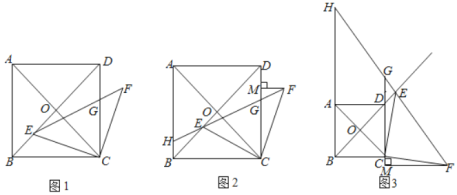
ШчЭМ1ЃЌЕуPдкОиаЮABCDЕФЖдНЧЯпACЩЯЃЌЧвВЛгыЕуAЃЌCжиКЯЃЌЙ§ЕуPЗжБ№зїБпABЃЌADЕФЦНааЯпЃЌНЛСНзщЖдБпгкЕуEЃЌFКЭGЃЌHЃЌШнвзжЄУїЫФБпаЮPEDHКЭЫФБпаЮPFBGЪЧУцЛ§ЯрЕШЕФОиаЮЃЌЗжБ№СЌНсEGЃЌFHЃЎ
ЂйИљОнОиаЮPEDHКЭОиаЮPFBGУцЛ§ЯрЕШЕФЙиЯЕЃЌФЧУДPEЁЄPH= ЃЎ
ЂкЧѓжЄЃКEGЁЮFHЃЎ
ЃЈ2ЃЉЗНЗЈЧЈвЦЃК
ШчЭМ2ЃЌвбжЊжБЯп ![]() ЗжБ№гыxжсЃЌyжсНЛгкDЃЌCСНЕуЃЌгыЫЋЧњЯп
ЗжБ№гыxжсЃЌyжсНЛгкDЃЌCСНЕуЃЌгыЫЋЧњЯп ![]() НЛгкAЃЌBСНЕуЃЎ ЧѓжЄЃКAC=BDЃЎ
НЛгкAЃЌBСНЕуЃЎ ЧѓжЄЃКAC=BDЃЎ
ЃЈ3ЃЉжЊЪЖгІгУЃК
ШчЭМ3ЃЌЗДБШР§КЏЪ§ ![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыОиаЮABCOЕФБпBCНЛгкЕуD,гыБпABНЛгкЕуE, жБЯпDEгыxжсЃЌyжсЗжБ№НЛгкЕуFЃЌG ЃЎШєОиаЮABCOЕФУцЛ§ЮЊ10ЃЌЁїODGгыЁїODFЕФУцЛ§БШЮЊ3ЃК5ЃЌдђk=________ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгыОиаЮABCOЕФБпBCНЛгкЕуD,гыБпABНЛгкЕуE, жБЯпDEгыxжсЃЌyжсЗжБ№НЛгкЕуFЃЌG ЃЎШєОиаЮABCOЕФУцЛ§ЮЊ10ЃЌЁїODGгыЁїODFЕФУцЛ§БШЮЊ3ЃК5ЃЌдђk=________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
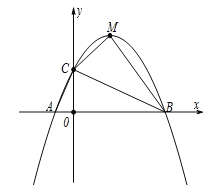
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() НЛxжсгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЎ
НЛxжсгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЕуAЁЂBЁЂCЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуMЮЊХзЮяЯпЕФЖЅЕуЃЌСЌНгBCЁЂCMЁЂBMЃЌЧѓЁїBCMЕФУцЛ§ЃЛ
ЃЈ3ЃЉСЌНгACЃЌдкxжсЩЯЪЧЗёДцдкЕуPЪЙЁїACPЮЊЕШбќШ§НЧаЮЃЌШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ![]() //
//![]() ЃЌЧвЗжБ№НЛЖдНЧЯпACгкЕуEЃЌFЃЌСЌНгBEЃЌDFЃЎ
ЃЌЧвЗжБ№НЛЖдНЧЯпACгкЕуEЃЌFЃЌСЌНгBEЃЌDFЃЎ
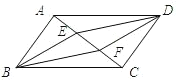
ЃЈ1ЃЉЧѓжЄЃКAE=CFЃЛ
ЃЈ2ЃЉШєBE=DEЃЌЧѓжЄЃКЫФБпаЮEBFDЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧЖЋФЯжнФГГЌЪаЙКНјМзЁЂввСНжжЩЬЦЗЃЌвбжЊЙКНј3МўМзЩЬЦЗКЭ2МўввЩЬЦЗЃЌаш60дЊЃЛЙКНј2МўМзЩЬЦЗКЭ3МўввЩЬЦЗЃЌаш65дЊЃЎ
ЃЈ1ЃЉМзЁЂввСНжжЩЬЦЗЕФНјЛѕЕЅМлЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉЩшМзЩЬЦЗЕФЯњЪлЕЅМлЮЊxЃЈЕЅЮЛЃКдЊ/МўЃЉЃЌдкЯњЪлЙ§ГЬжаЗЂЯжЃКЕБ11ЁмxЁм19ЪБЃЌМзЩЬЦЗЕФШеЯњЪлСПyЃЈЕЅЮЛЃКМўЃЉгыЯњЪлЕЅМлxжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌxЁЂyжЎМфЕФВПЗжЪ§жЕЖдгІЙиЯЕШчБэЃК
ЯњЪлЕЅМлxЃЈдЊ/МўЃЉ | 11 | 19 |
ШеЯњЪлСПyЃЈМўЃЉ | 18 | 2 |
ЧыаДГіЕБ11ЁмxЁм19ЪБЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшМзЩЬЦЗЕФШеЯњЪлРћШѓЮЊwдЊЃЌЕБМзЩЬЦЗЕФЯњЪлЕЅМлxЃЈдЊ/МўЃЉЖЈЮЊЖрЩйЪБЃЌШеЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
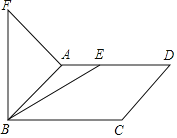
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌABЃН2ЃЌЁЯABCЃН45ЁуЃЌЕуEЮЊЩфЯпADЩЯвЛЖЏЕуЃЌСЌНгBEЃЌНЋBEШЦЕуBФцЪБеыа§зЊ60ЁуЕУЕНBFЃЌСЌНгAFЃЌдђAFЕФзюаЁжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() ШЦ
ШЦ![]() ЕуЫГЪБеыа§зЊ
ЕуЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЯпЖЮ![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯвЛЕуЃЌЯпЖЮ
ЩЯвЛЕуЃЌЯпЖЮ![]() ЕФбгГЄЯпНЛжБЯп
ЕФбгГЄЯпНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ДЙжБжБЯп
ДЙжБжБЯп![]() гкЕу
гкЕу![]() ЃЌЧыжБНгаДГіЯпЖЮ
ЃЌЧыжБНгаДГіЯпЖЮ![]() ЕФЪ§СПЙиЯЕ.
ЕФЪ§СПЙиЯЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌABЮЊ
жаЃЌABЮЊ![]() ЕФжБОЖЃЌCЮЊ
ЕФжБОЖЃЌCЮЊ![]() ЩЯвЛЕуЃЌPЪЧ
ЩЯвЛЕуЃЌPЪЧ![]() ЕФжаЕуЃЌЙ§ЕуPзїACЕФДЙЯпЃЌНЛACЕФбгГЄЯпгкЕуDЃЎ
ЕФжаЕуЃЌЙ§ЕуPзїACЕФДЙЯпЃЌНЛACЕФбгГЄЯпгкЕуDЃЎ
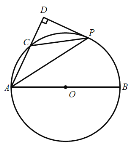
ЃЈ1ЃЉЧѓжЄЃКDPЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAC=5ЃЌ![]() ,ЧѓAPЕФГЄЃЎ
,ЧѓAPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
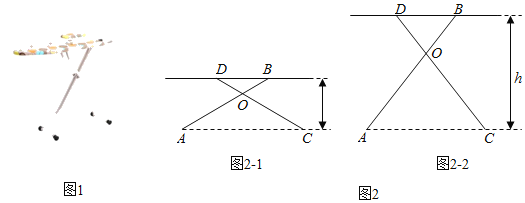
ЁОЬтФПЁПгавЛжжЩ§НЕьйЬЬЬЈШчЭМ1ЫљЪОЃЌЦфдРэЪЧЭЈЙ§ИФБфСНИљжЇГХИЫМаНЧЕФЖШЪ§РДЕїећьйЬЬЬЈЕФИпЖШЃЎЭМ2ЪЧетжжЩ§НЕьйЬЬЬЈЕФЦНУцЪОвтЭМЃЎABКЭCDЪЧСНИљЯрЭЌГЄЖШЕФЛюЖЏжЇГХИЫЃЌЕуOЪЧЫќУЧЕФСЌНгЕуЃЌOA=OCЃЌhЃЈcmЃЉБэЪОьйЬЬЬЈЕФИпЖШЃЎ
ЃЈ1ЃЉШчЭМ2Љ1ЃЎШєAB=CD=110cmЃЌЁЯAOC=120ЁуЃЌЧѓhЕФжЕЃЛ
ЃЈ2ЃЉАЎЖЏФдНюЕФаЁУїЗЂЯжЃЌЕБМвРяетжжЩ§НЕьйЬЬЬЈЕФИпЖШЮЊ120cmЪБЃЌСНИљжЇГХИЫЕФМаНЧЁЯAOCЪЧ74ЁуЃЈШчЭМ2Љ2ЃЉЃЎЧѓИУьйЬЬЬЈжЇГХИЫABЕФГЄЖШЃЈНсЙћОЋШЗЕНlcmЃЉЃЎ
ЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.6ЃЌcos37ЁуЁж0.8ЃЌsin53ЁуЁж0.8ЃЌcos53ЁуЁж0.6ЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com