
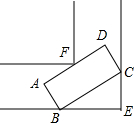
 如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 先设平板手推车的长度不能超过x米,则得出x为最大值时,平板手推车所形成的三角形CBE为等腰直角三角形.连接EF,与BC交于点G,利用△CBE为等腰直角三角形即可求得平板手推车的长度不能超过多少米.
解答 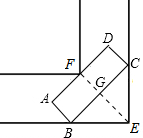 解:设平板手推车的长度不能超过x米,则x为最大值,且此时平板手推车所形成的三角形CBE为等腰直角三角形.
解:设平板手推车的长度不能超过x米,则x为最大值,且此时平板手推车所形成的三角形CBE为等腰直角三角形.
连接EF,与BC交于点G.
∵直角走廊的宽为1.5m,
∴EF=$\frac{3}{2}\sqrt{2}$(m),
∴GE=EF-FG=$\frac{3}{2}\sqrt{2}$-1(m).
又∵△CBE为等腰直角三角形,
∴AD=BC=2CG=2GE=3$\sqrt{2}$-2≈2.2(m).
故答案为:2.2
点评 本题主要考查了勾股定理的应用以及等腰三角形知识,解答的关键是由题意得出要想顺利通过直角走廊,此时平板手推车所形成的三角形为等腰直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com