
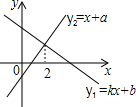 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①. 科目:初中数学 来源: 题型:选择题
| A. | 若y1<y2,则x1<x2 | |
| B. | 若y1-y2=2,则x1-x2=-1 | |
| C. | 可由直线y=2x向上平移4个单位得到 | |
| D. | 与坐标系围成的三角形面积为8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
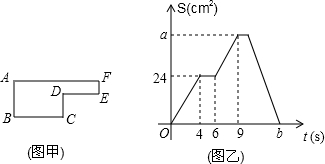
 小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.
小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
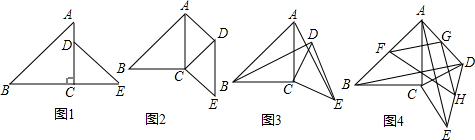 问题情境:
问题情境:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
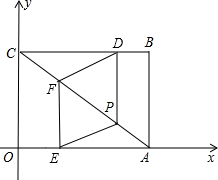 在直角坐标系中,点O为原点,点B的坐标为(4,3),四边形ABCO是矩形,点D从B出发以每秒1个单位的速度向终点C运动,同时点E从O点出发以每秒1个单位的速度向终点A运动,过D作DP⊥BC与AC交于点P,过E作EF⊥AO与AC交于点F,连结DF、PE.
在直角坐标系中,点O为原点,点B的坐标为(4,3),四边形ABCO是矩形,点D从B出发以每秒1个单位的速度向终点C运动,同时点E从O点出发以每秒1个单位的速度向终点A运动,过D作DP⊥BC与AC交于点P,过E作EF⊥AO与AC交于点F,连结DF、PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com