
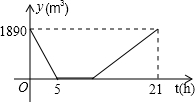
 (2013•嘉定区二模)某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:
(2013•嘉定区二模)某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:| 1 |
| 2 |
|


科目:初中数学 来源: 题型:
 |
| AB |
 |
| CB |
| CF |
| AF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•嘉定区二模)如图,点E是正方形ABCD边BC上的一点(不与B、C重合),点F在CD边的延长线上,且满足DF=BE.联结EF,点M、N分别是EF与AC、AD的交点.
(2013•嘉定区二模)如图,点E是正方形ABCD边BC上的一点(不与B、C重合),点F在CD边的延长线上,且满足DF=BE.联结EF,点M、N分别是EF与AC、AD的交点.| CE |
| CM |
| AC |
| FC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•嘉定区二模)已知平面直角坐标系xOy(如图),抛物线y=
(2013•嘉定区二模)已知平面直角坐标系xOy(如图),抛物线y=| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com