
【题目】为了了解某校九年级学生的课外数学学习时长情况,该校将选取部分学生进行调查,以下样本中,最具代表性的是( )
A.该年级篮球社团的学生
B.该年级数学成绩前![]() 名的女生
名的女生
C.该年级跑步较快的学生
D.从每个班级中,抽取学号为![]() 的整数倍的学生
的整数倍的学生
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后,随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵,B:5棵,C:6棵,D:7棵,并将各类的人数绘制了扇形统计图(如图1)和条形统计图(如图2),请根据相关信息解答下列问题:
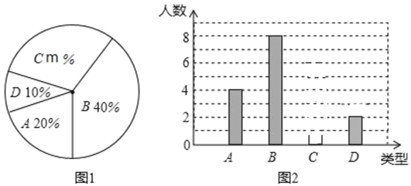
(1)图1中m的值为 ;
(2)补全图2,并求出抽查的20名学生每人植树量数据的众数、中位数;
(3)求抽查的20名学生平均每人的植树量(保留一位小数),并估计全校260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
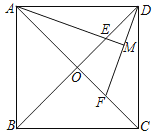
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
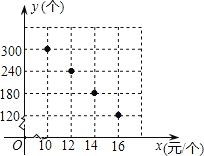
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调査.这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
(1)试求出y与x之间的函数关系;
(2)若许原瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() 且与
且与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 是第一象限内抛物线上一点,过点
是第一象限内抛物线上一点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 当
当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,若点
的条件下,若点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,当以点
在抛物线的对称轴上,当以点![]() 为顶点的四边形是平行四边形时,求出所有符合条件的点
为顶点的四边形是平行四边形时,求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
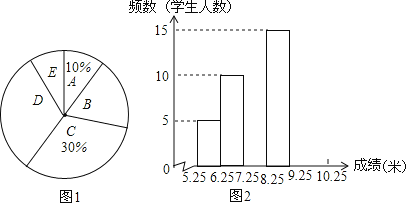
【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).
(1)抽取的这部分男生有______人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在_____组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣![]() x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求抛物线表达式;
(2)点P为抛物线上的一个动点,过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点,若P、M、N三点中恰有一点是其他两点所连线段的中点(三点重合除外),请求出此时点P的坐标.
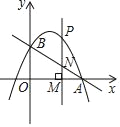
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com