
【题目】陈老师从拉面的制作中受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段![]() ,对折后(点
,对折后(点![]() 与
与![]() 重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段
重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段![]() 上的
上的![]() 和
和![]() 均变成
均变成![]() ,
,![]() 变成1等).那么在线段
变成1等).那么在线段![]() 上(除
上(除![]() 、
、![]() )的点中,在第
)的点中,在第![]() 次操作后,恰好被拉到与1重合的点所对应的数为________________.
次操作后,恰好被拉到与1重合的点所对应的数为________________.
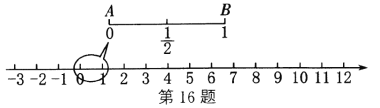
【答案】![]()
【解析】
根据题意,可知下一次的操作把上一次的对应点正好扩大了2倍.因为第一次操作后,
原线段AB上的![]() ,
,![]() 均变成
均变成![]() ,则第二次操作后,恰好被拉到与1重合的点所对应的数是
,则第二次操作后,恰好被拉到与1重合的点所对应的数是![]() 和
和![]() ,则它们的和可求.根据题意,将恰好被拉到与1重合的点所对应的坐标列出数据,找出规律,列出通式即可.
,则它们的和可求.根据题意,将恰好被拉到与1重合的点所对应的坐标列出数据,找出规律,列出通式即可.
根据题意,得
操作次数 变化点 重合点 | 1 | 2 | 3 | 4 |
1 |
|
|
|
|
1 |
|
|
|
第一次操作后,原线段AB上的![]() 变为1,
变为1,
第二次操作后,恰好被拉到与1重合的点所对应的数有21=2个,分别是![]() 和
和![]() ,其和为1,
,其和为1,
第三次操作后,恰好被拉到与1重合的点所对应的数有22=4个,分别是![]() 、
、![]() 、
、![]() 和
和![]() ,其和为2,
,其和为2,
…,
可以推出第n次操作后,恰好被拉到与1重合的点所对应的数的通式为![]() 、
、![]() …
…![]() ,
,
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是( ) 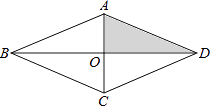
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
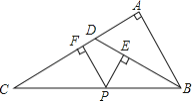
【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
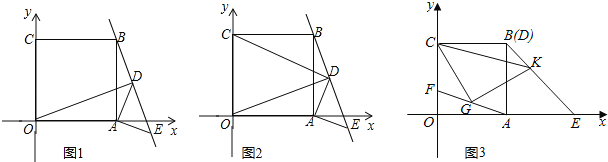
【题目】在平面直角坐标系中,正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上.
(1)如图1,连接OD,求证:△OAD≌△BAE;
(2)如图2,连接CD,求证:BE﹣![]() DE=
DE=![]() CD;
CD;
(3)如图3,当图1中的Rt△ADE的顶点D与点B重合时,点E正好落在x轴上,F为线段OC上一动点(不与O、C重合),G为线段AF的中点,若CG⊥GK交BE于点K时,请问∠KCG的大小是否变化?若不变,请求其值;若改变,求出变化的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有 A,B 两种商品.已知在打折前,买 20 件 A 商品和 10 件B 商品用了 400 元;买 30 件 A 商品和 20 件 B 商品用了 640 元.A,B 两种商品打相同折以后,某人买 100 件 A 商品和 200 件 B 商品一共比不打折少花 640 元,计算打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=kx+b的图象如图所示,则k,b的值可能为( )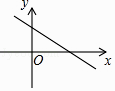
A.k=3,b=3
B.k=3,b=﹣3
C.k=﹣3,b=3
D.k=﹣3,b=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.请你根据图象,回答下列问题: 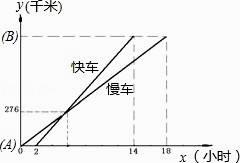
(1)慢车比快车早出发小时,快车追上慢车时行驶了千米,快车比慢车早小时到达B地;
(2)在下列3个问题中任选一题求解(多做不加分): ①快车追上慢车需几个小时?
②求慢车、快车的速度;
③求A、B两地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
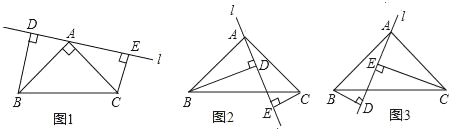
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com