
分析 根据按一定规律排列的一列数依次为:$\frac{2}{3}$,$\frac{5}{5}$,$\frac{8}{7}$,$\frac{11}{9}$,$\frac{14}{11}$,$\frac{17}{13}$,…,可得第n个数为$\frac{3n-1}{2n+1}$,据此可得第100个数.
解答 解:按一定规律排列的一列数依次为:$\frac{2}{3}$,$\frac{5}{5}$,$\frac{8}{7}$,$\frac{11}{9}$,$\frac{14}{11}$,$\frac{17}{13}$,…,
按此规律,第n个数为$\frac{3n-1}{2n+1}$,
∴当n=100时,$\frac{3n-1}{2n+1}$=$\frac{299}{201}$,
即这列数中的第100个数是$\frac{299}{201}$,
故答案为:$\frac{299}{201}$.
点评 本题考查了数字变化类问题,解决问题的关键是找出变化规律,认真观察、仔细思考,善用联想是解决这类问题的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
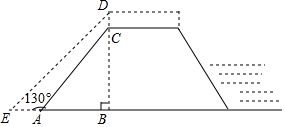 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.
为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
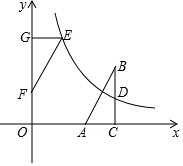 如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC边的中点D(3,1).
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC边的中点D(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28米 | B. | 48米 | C. | 57米 | D. | 88米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=ax2+2ax+a-1(a>0).
已知二次函数y=ax2+2ax+a-1(a>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com