
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
【答案】(1)工程队在使用新设备后每天能修路45米.(2)当m=26,n=16时,修建这条公路的总费用最少,最少费用为816000元.
【解析】
试题分析:(1)设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50)x=1.5x(米),根据题意,列出方程![]() ,即可解答;
,即可解答;
(2)设修建这条公路的总费用为W元,则W=16000m+25000n,由30m+45n=1500,得到m=![]() ,则W=16000×
,则W=16000×![]() +25000n=800000+1000n,根据16≤n≤26,利用一次函数的增减性即可解答.
+25000n=800000+1000n,根据16≤n≤26,利用一次函数的增减性即可解答.
解:(1)设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50)x=1.5x(米),
根据题意得:![]() ,
,
解得:x=30,
当x=30时,1.5x≠0,
∴x=30是分式方程的解,
1.5x=45,
答:工程队在使用新设备后每天能修路45米.
(2)设修建这条公路的总费用为W元,
则W=16000m+25000n,
∵30m+45n=1500,
∴m=![]() ,
,
把m=![]() 代入W=16000m+25000n得;
代入W=16000m+25000n得;
W=16000×![]() +25000n=800000+1000n,
+25000n=800000+1000n,
∵k=1000>0,
∴W随n的增大而增大,
∵16≤n≤26,
∴当n=16时,W有最小值,最小值为;800000+16000=816000(元),
m=![]() =26,
=26,
答:当m=26,n=16时,修建这条公路的总费用最少,最少费用为816000元.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
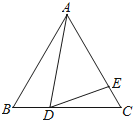
(1)求证:△ABD∽△DCE.
(2)若AB=9cm,BD=3cm,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周长是( )

A.10 B.15 C.20 D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与数 表示的点重合;
(2)若﹣1表示的点与3表示的点重合,5表示的点与数 表示的点重合;
(3)若数轴上A、B两点之间的距离为c个单位长度,点A表示的有理数是a,并且A、B两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com