
【题目】如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转一定角度(小于360°)得到△B′AC′.
(1)若点B′落在线段AC上,在图中画出△B′AC′,并直接写出当AC=4时,CC′的值;
(2)若∠ACB=20°,旋转后,B′C′⊥AC,请直接写出旋转角的度数.

【答案】(1)4![]() ;(2)70°或250°.
;(2)70°或250°.
【解析】
(1)如图1中,△B′AC′如图所示;作AH⊥CC′于H.只要证明CH=HC′,只要求出CH的长即可解决问题;
(2)如图2,分两种情况讨论.
(1)如图1中,△B′AC′如图所示;作AH⊥CC′于H.
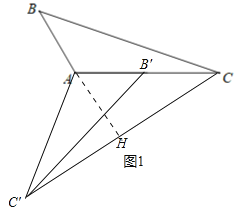
∵AC=AC′=4,∠C′AC=∠CAB=120°,AH⊥CC′,∴CH=HC′,∠CAH=![]() ∠CAC′=60°,∠ACH=30°,∴AH=
∠CAC′=60°,∠ACH=30°,∴AH=![]() AC=2,∴CH=
AC=2,∴CH=![]() =2
=2![]() ,∴CC′=4
,∴CC′=4![]() .
.
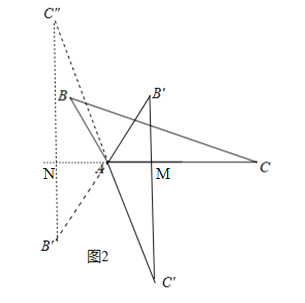
(2)如图2中,如图所示,分两种情况讨论:
①当B旋转到B′时.
∵B′C′⊥AC,∠C′=∠C=20°,∴∠C′AM=90°-∠C′=90°-20°=70°,∴旋转角为70°;
②当B旋转到B″时,同理可得:∠NAC″=70°.
∵∠B″AC″=∠BAC=120°,∴∠NAB″=120°-70°=50°.
∵∠BAN=180°-120°=60°,∴∠BAB″=60°+50°=110°,∴旋转角=360°-110°=250°.
综上所述:旋转角的度数为70°或250°.


科目:初中数学 来源: 题型:
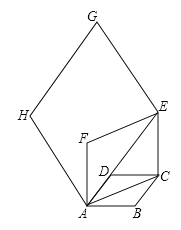
【题目】如图,边长为![]() 的菱形
的菱形![]() 中,
中,![]() .连结对角线
.连结对角线![]() ,以
,以![]() 为边作第二个菱形
为边作第二个菱形![]() ,使
,使![]() .连结
.连结![]() ,再以
,再以![]() 为边作第三个菱形
为边作第三个菱形![]() ,使
,使![]() ,一按此规律所作的第
,一按此规律所作的第![]() 个菱形的边长是__________.
个菱形的边长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年“清明节”前夕,宜宾某花店用1000元购进若干菊花,很快售完,接着又用2500元购进第二批
花,已知第二批所购花的数量是第一批所购花数的2倍,且每朵花的进价比第一批的进价多![]() 元.
元.
(1)第一批花每束的进价是多少元.
(2)若第一批菊花按3元的售价销售,要使总利润不低于1500元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
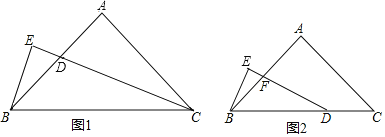
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元
元![]() 公里计算,耗时费按
公里计算,耗时费按![]() 元
元![]() 分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:
分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:

平均速度(公里/时) | 里程数(公里) | 车费(元) | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
(1)求![]() ,
,![]() 的值;
的值;
(2)如果你采用“滴滴出行”的打车方式,保持平均车速![]() 公里
公里![]() 时,行驶了
时,行驶了![]() 公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
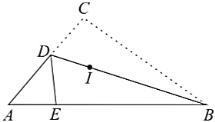
【题目】如图,三角形纸片![]() 中,沿过
中,沿过![]() 点的直线折叠这个三角形,使点
点的直线折叠这个三角形,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,则下列结论:
,则下列结论:
①![]() 平分
平分![]() ;
;
②![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为7;
的周长为7;
④![]() ;
;
⑤若![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,
时,![]() .其中结论正确的有( )
.其中结论正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
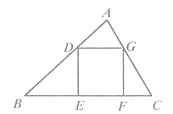
【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A. ![]() B.
B. ![]() C. 2 D. 2
C. 2 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
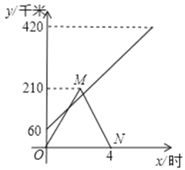
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com