
 ?
?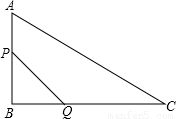
 ×BP×BQ.而BP=AB-AP=6-t,BQ=2t,代入即可求出S与t的函数关系式,由P点只能从A出发沿边AB向点B移动,可知t的取值范围;
×BP×BQ.而BP=AB-AP=6-t,BQ=2t,代入即可求出S与t的函数关系式,由P点只能从A出发沿边AB向点B移动,可知t的取值范围; ,那么
,那么 ,又AP=t,BP=6-t,BQ=2t,CQ=12-2t,根据三角形的面积公式可知,只需求出△APM中AP边上的高及△MQC中CQ边上的高,即可根据等量关系列出方程,进而求出方程的解.为此,作MD⊥AB于D,ME⊥BC于E.根据中位线的判定及性质可求出DM、ME的值.
,又AP=t,BP=6-t,BQ=2t,CQ=12-2t,根据三角形的面积公式可知,只需求出△APM中AP边上的高及△MQC中CQ边上的高,即可根据等量关系列出方程,进而求出方程的解.为此,作MD⊥AB于D,ME⊥BC于E.根据中位线的判定及性质可求出DM、ME的值. (3分)
(3分)
 (5分)
(5分)
 .
. s时,△PBQ与△ABC相似;(6分)
s时,△PBQ与△ABC相似;(6分) ,
,
 ,即D是AB的中点,(7分)
,即D是AB的中点,(7分) .
. ,(8分)
,(8分) ,
, ,(9分)
,(9分)
 (1分)
(1分)

科目:初中数学 来源:2010年辽宁省大连市中考数学一模试卷(解析版) 题型:解答题
 ,求抛物线的解析式.
,求抛物线的解析式.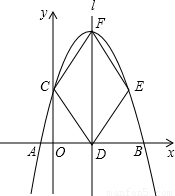
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省大连市中考数学一模试卷(解析版) 题型:解答题
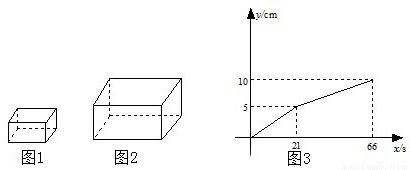
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省大连市中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com