
����Ŀ��ijСѧ��չ�������ǻ��ѧ�����Դ���������������������������������������Т����������ѡһ����Ŀ�μ����Ǿ�ѡ�����ݸ�Уһ�꼶ij��ѧ������������������������Ƴ�������������������ͳ��ͼ�������ͼ����Ϣ�ش��������⣺
��1���μӵ����ѧ�������� ���ˣ�
��2��������ͳ��ͼ����������
��3�����������ͳ��ͼ��������������Ӧ������Բ�ĽǶ�����
��4�����ݵ��������Թ��Ƹ�СѧȫУ3600��ѧ��������������������ѧ��������
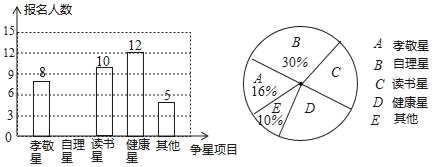
���𰸡���1��50����2����ͼ����������3��72�㣻��4����СѧȫУ3600��ѧ��������������������ѧ������Ϊ864�ˣ�
��������
����Т���ǵ���������ռ�ٷֱȿɵñ������ѧ��������
������������ȥ�������������=�����ǵ��������ٲ�ͼ���ɣ�
�����C��ռ�ٷֱȣ�����360���C��ռ�ٷֱȿɵô𰸣�
���ȼ���������н����ǵ�ѧ����ռ�ٷֱȣ�������������������ķ������㼴�ɣ�
��1���μӵ����ѧ������8��16%=50�ˣ�
�ʴ�Ϊ��50��
��2������������������Ϊ50��30%=15�ˣ�
��ȫͼ�����£�
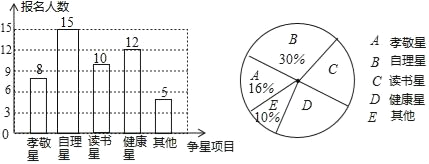
��3������ͳ��ͼ��������������Ӧ������Բ�ĽǶ���Ϊ360���![]() =72�㣻
=72�㣻
��4��3600��![]() =864��
=864��
�𣺸�СѧȫУ3600��ѧ��������������������ѧ������Ϊ864�ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
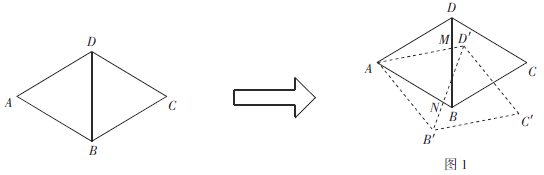
�����龳����һ���ۺ�ʵ������ϣ�ͬѧ��������Ϊ�����о�������ת�е����⣺
��֪��������ABCD�У�BDΪ�Խ��ߣ�![]() ��AB=4��������ABCD�ƶ���A˳ʱ����ת����ת��Ϊ
��AB=4��������ABCD�ƶ���A˳ʱ����ת����ת��Ϊ![]() ����λ��������ת�������Ϊ
����λ��������ת�������Ϊ![]() ������ת̽���������������⣬��������ǽ����
������ת̽���������������⣬��������ǽ����
�۲�֤����
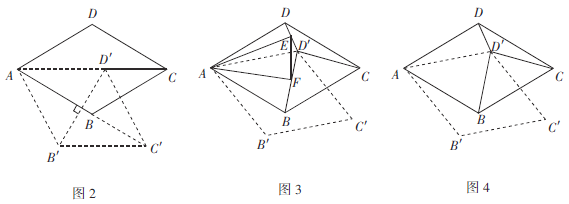
��1����ͼ1������ת��![]() ��
��![]() ��BD�ཻ�ڵ�M��AB��
��BD�ཻ�ڵ�M��AB��![]() �ཻ�ڵ�N����˵���߶�DM��
�ཻ�ڵ�N����˵���߶�DM��![]() ��������ϵ��
��������ϵ��
�������㣺
��2����ͼ2������![]() ������ABCD��ת�Ĺ����У���
������ABCD��ת�Ĺ����У���![]() ��AB���ഹֱʱ��
��AB���ഹֱʱ��![]() �ij�Ϊ ��
�ij�Ϊ ��
��3����ͼ3������ת��![]() ���ֱ�����
���ֱ�����![]() ��
��![]() ������A�ֱ���
������A�ֱ���![]() ��
��![]() ������EF������ABCD��ת�Ĺ����У�������
������EF������ABCD��ת�Ĺ����У�������![]() �д��ڳ��Ȳ�����߶�EF�������EF���ȣ�
�д��ڳ��Ȳ�����߶�EF�������EF���ȣ�
����̽����
��4����ͼ4���ڣ�3���������£����ж���![]() ��
��![]() ��
��![]() �����߶γ���Ϊ�ߵ���������ʲô���������Σ���˵�����ɣ�
�����߶γ���Ϊ�ߵ���������ʲô���������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У���P(x��y)�ĺᡢ������ľ���ֵ֮�ͽ�����P(x��y)�Ĺ���ֵ����[P]��|x|+|y|��
(1)��֪M(p��2p)�ڷ���������y��![]() ��ͼ���ϣ���[M]��3�����������Ľ���ʽ��
��ͼ���ϣ���[M]��3�����������Ľ���ʽ��
(2)��֪��A��ֱ��y��x+2�ϵĵ㣬��[A]��4�����A�����ꣻ
(3)��������y��ax2+bx+1��ֱ��y��xֻ��һ������C����֪��C�ڵ�һ���ޣ���2��[C]��4����t��2b2��4a+2020����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
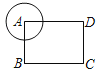
����Ŀ����ͼ���ھ���ABCD�У�AB��6��AD��8���Զ���AΪԲ�����뾶Ϊr��Բ����Ҫ��������������������һ����Բ�ڣ���������һ����Բ�⣬��r��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ֱ������ƽ���ڣ���֪��O�İ뾶ΪR����AΪ��O������һ�㣬����B��Բ��O�ľ���Ϊm���߶�AB�ij���Ϊl����m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ������m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ����
��2����ͼ����O�İ뾶Ϊ2����P�ġ�Kֵ���������£�����QΪ��O������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P�ġ�Kֵ������ΪKP���ر�أ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0��
������A��6��8����B����1��0������KA���� ����KB���� ����
����ֱ��y��2x��1�ϴ��ڵ�P��ʹ![]() �������P�ĺ����ꣻ
�������P�ĺ����ꣻ
��ֱ��![]() ��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��
��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��![]() ������ֱ��д��b��ȡֵ��Χ��
������ֱ��д��b��ȡֵ��Χ��
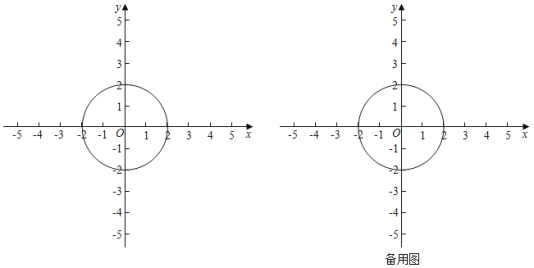
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲����
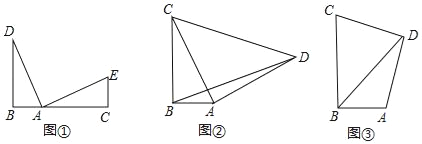
��ͼ�ٵ�B��A��C��ͬһ��ֱ���ϣ�DB��BC��EC��BC�ҡ�DAE=90�㣬AD=AE����BC��BD��CE֮���������ϵΪ��
��2��������
��ͼ�ڣ���Rt��ABC�У���ABC=90�㣬CB=4��AB=2����ACΪֱ�DZ�����������Rt��DAC������BD����BD�ij���
��3����չ����
��ͼ�ۣ����ı���ABCD�У���ABC=��ADC=90�㣬CB=4��AB=2��DC=DA����ֱ��д��BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˳��мס����������Ѳ�ժ���������ۼ۸���ͬ�������ڼ䣬���Ҳ�ժ�Ƴ��Żݷ����������Żݷ����ǣ��οͽ��蹺����Ʊ����ժ�����������Żݣ������Żݷ����ǣ��οͽ����蹺����Ʊ����ժ�����Ѱ��ۼ۸���Ż��ڼ䣬���ο͵����Ѳ�ժ��Ϊ![]() ��ǧ�ˣ����ڼ������ܷ���Ϊ
��ǧ�ˣ����ڼ������ܷ���Ϊ![]() ����Ԫ�������������ܷ���Ϊ
����Ԫ�������������ܷ���Ϊ![]() ����Ԫ����
����Ԫ����![]() ����
����![]() ����
����![]() ֮��ĺ�����ϵ��ͼ��ʾ��
֮��ĺ�����ϵ��ͼ��ʾ��
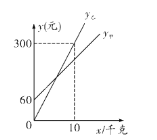
��1����![]() ����
����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������ڼ䣬����һ��������ȥ������ժ���ѣ���ժ�����Ѻ���һ��֧�����ã�������һ��Ӧѡ���ļ����������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС����չ�����г���ȫ������������Ļ���Ե��³������˸Ľ�����ͼ����С��ԭ���³������ڴ���б��AC��Ϊ13�ף������¶�Ϊi��1��2.4��AB��BC��Ϊ�˾����г���ȫ���ֽ�б�µ��½Ǹ�Ϊ13��������ADC��13������ʱ��B��C��D��ͬһֱ���ϣ���
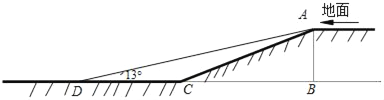
��1�����������ĸ߶�AB��
��2����б�¸Ľ�������D��ԭ���C�ľ��루�����ȷ��0.1�ף���
���ο����ݣ�sin13���0.225��cos13���0.974��tan13���0.231��cot13���4.331��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ��������C��0����4����������![]() ��
��![]() ����x���ཻ��A����2��0����B���㣮
����x���ཻ��A����2��0����B���㣮

��1��a 0��![]() 0���������������
0���������������
��2�����������߹���ֱ��x=2�Գƣ��������ߵĺ�������ʽ��
��3���ڣ�2���������£�����AC��E����������һ���㣬����E��AC��ƽ���߽�x���ڵ�F���Ƿ���������ĵ�E��ʹ����A��C��E��FΪ��������ɵ��ı�����ƽ���ı��Σ������ڣ�������������ĵ�E�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com