
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,设计开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数;
(2)将条形图补充完整;
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数。
科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=-x-2交x轴于点A,交y轴于点B,抛物线y2=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)求当y1≥y2时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图①,在△ABC中,∠ACB=2∠B,AD为∠BAC的角平分线,
求证:AB=AC+CD
小明同学经过思考,得到如下解题思路:
在AB上截取AE=AC,连接DE,得到△ADE≌△ADC,从而易证AB=AC+CD
(1)请你根据以上解思路写出证明过程;
(2)如图②,若AD为△ABC的外角∠CAE平分线,交BC的延长线于点D,
∠D=25°,其他条件不变,求∠B的度数。


查看答案和解析>>
科目:初中数学 来源: 题型:
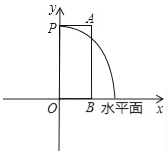
【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程x2+4x﹣5=0的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com