
【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
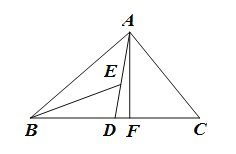
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,![]() ,AD是BC边上的高,如果
,AD是BC边上的高,如果![]() ,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
(1)若![]() ,
,![]() ,则△ABC____ “高和三角形”(填“是”或“不是”);
,则△ABC____ “高和三角形”(填“是”或“不是”);
(2)一般地,如果△ABC是“高和三角形”,则![]() 与
与![]() 之间的关系是____,并证明你的结论
之间的关系是____,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=115°,那么∠BFD的度数是
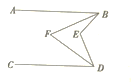
A.62°B.64°C.57.5°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
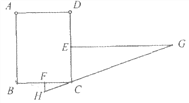
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
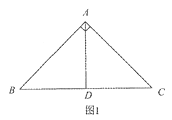
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com