
����Ŀ�����壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
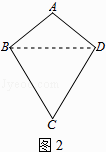
��1����֪����ͼ1���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C����A=70�㣬��B=80�㣮���C����D�Ķ�����
��2����̽�����ȶԽ��ı��Ρ�����ʱ����ͬѧ����һ�����ȶԽ��ı��Ρ�ABCD����ͼ2�������С�ABC=��ADC��AB=AD����ʱ������CB=CD����������֤���˽��ۣ�
��3����֪���ڡ��ȶԽ��ı��Ρ�ABCD�У���DAB=45�㣬��ABC=90�㣬AB=5��AD=4 ![]() ����Խ���AC�ij�Ϊ ��
����Խ���AC�ij�Ϊ ��
���𰸡�
��1��
�⣺���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C��
���D=��B=80�㣬
���C=360�㩁��A����B����D=360�㩁70�㩁80�㩁80��=130�㣻
��2��
֤������ͼ2��ʾ������BD��
��AB=AD��
���ABD=��ADB��
�ߡ�ABC=��ADC��
���ABC����ABD=��ADC����ADB��
���CBD=��CDB��
��CB=CD��
��3��![]()
����������3���⣺�����������
�ٵ���ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E����ͼ3��ʾ��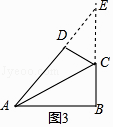
�ߡ�ABC=90�㣬��DAB=45�㣬AB=5�����E=45�㣬
��AE= ![]() AB=5
AB=5 ![]() ��
��
��DE=AE��AD=5 ![]() ��4
��4 ![]() �T
�T ![]() ��
��
�ߡ�EDC=90�㣬��E=45�㣬
��CD= ![]() ��
��
��AC= ![]() =
= ![]() =
= ![]() ��
��
�ڵ���BCD=��DAB=45��ʱ��
����D��DM��AB�ڵ�M��DN��BC�ڵ�N����ͼ4��ʾ��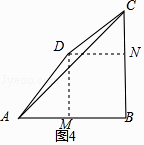
���AMD=90�㣬�ı���BNDM�Ǿ��Σ�
�ߡ�DAB=45�㣬
���ADM=45�㣬
��AM=DM= ![]() AD=4��
AD=4��
��BM=AB��AM=5��4=1��
���ı���BNDM�Ǿ��Σ�
��DN=BM=1��BN=DM=4��
�ߡ�BCD=45�㣬
��CN=DN=1��
��BC=CN+BN=5��
��AC= ![]() =5
=5 ![]() ��
��
�ʴ���������ڣ�
����������AC�ij�Ϊ ![]() ��
��
���Դ��ǣ� ![]() ��
��
��1�������ı���ABCD�ǡ��ȶԽ��ı��Ρ��ó���D=��B=80�㣬���ݶ�����ڽǺͶ��������C���ɣ���2������BD����AB=AD���ó���ABD=��ADB��֤����CBD=��CDB�����ɵó�CB=CD����3��������������ٵ���ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E�����õ���ֱ�������ε��������AE���ó�DE���������Ǻ������CD���ɹ��ɶ������AC���ڵ���BCD=��DAB=45��ʱ������D��DM��AB�ڵ�M��DN��BC�ڵ�N�����AMD=90�㣬�ı���BNDM�Ǿ��Σ������AM��DM�����ɾ��ε����ʵó�DN=BM=1��BN=DM=4�����CN��BC�����ݹ��ɶ������AC���ɣ�
�����㾫����ͨ��������õ���ֱ�������κ��ɶ����ĸ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��һ��ֽƬ����C=90�㣬AC=6��BC=8���ֽ����۵���ʹ��B���A�غϣ��ۺ�ΪDE����DE�ij�Ϊ�� ��
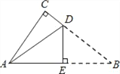
A. 1.75 B. 3 C. 3.75 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴�������� ![]() ��ͼ����A����2��1����B��1��n�����㣮
��ͼ����A����2��1����B��1��n�����㣮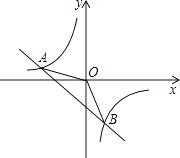
��1����ȷ������������������һ�κ����ı���ʽ��
��2�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����:
����֪��:һ���߶��������˵㣬�߶�![]() ���߶�
���߶�![]() ��ʾͬһ���߶�. ����ֱ��
��ʾͬһ���߶�. ����ֱ��![]() ��ȡ��������ͬ�ĵ㣬��������Ϊ�˵���߶ι��� ��;��ȡ���ĸ���ͬ�ĵ㣬�����߶� ��;��;�������ƣ�ȡ��
��ȡ��������ͬ�ĵ㣬��������Ϊ�˵���߶ι��� ��;��ȡ���ĸ���ͬ�ĵ㣬�����߶� ��;��;�������ƣ�ȡ��![]() ����ͬ�ĵ㣬�����߶���.(�ú�
����ͬ�ĵ㣬�����߶���.(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
���̽��:
��һ����ǵĶ���Ϊ�˵�������ǵ��ڲ�������.
(1)�������������ߣ�������ͼ���й��� �����;
(2)������![]() �����ߣ�������ͼ���й��� �����.(�ú�
�����ߣ�������ͼ���й��� �����.(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
��չӦ��:
һ����·�Ϲ���8����վ����һ�л����������б���ͣ��ÿ����վ������·����Ϊ������·�������ֳ�Ʊ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ij�����㣬����ʼ�����x��ֵΪ18�����Ƿ��ֵ�1�εõ��Ľ��Ϊ9����2�εõ��Ľ��Ϊ14����3�εõ��Ľ��Ϊ7��������̽����2016�εõ��Ľ��Ϊ![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�AB��x���ϣ���B��ԭ��O�غϣ���֪��A����2��0����AC= ![]() ������ABC��x������ƽ�ƣ�����C�Ķ�Ӧ��C1����ֱ��y=2x��4��ʱ����ƽ�Ƶľ����ǣ� ��
������ABC��x������ƽ�ƣ�����C�Ķ�Ӧ��C1����ֱ��y=2x��4��ʱ����ƽ�Ƶľ����ǣ� ��
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̴�λ���ҹ��������ˣ����㷢���ң���60��ʱ��ɵġ�ֱָ�㷨ͳ�ڡ��Ƕ����Ŵ���ѧ�����������˴�ͳ���������ȷ���������÷����������������⣺
һ����ͷһ��ɮ����ɮ������������
Сɮ���˷�һ������С���еü�����
��˼�ǣ���100�����з�100����ͷ����������1�˷�3����С����3�˷�1�������÷��꣬��С���и��ж����ˣ������������ȷ���ǣ�������

A. �����25�ˣ�С����75�� B. �����75�ˣ�С����25��
C. �����50�ˣ�С����50�� D. ��С���и�100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��![]() �£�a��
�£�a��![]() ����
����
��1������A��
��2����a��3ʱ���Ǵ�ʱA��ֵΪf��3������a��4ʱ���Ǵ�ʱA��ֵΪf��4�����������x�IJ���ʽ��![]() ��f��3��+f��4��+��+f��11���������⼯�������ϱ�ʾ������
��f��3��+f��4��+��+f��11���������⼯�������ϱ�ʾ������
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�߳�Ϊ2���ı���DEFG��ƽ���ı��Σ�DG=2��DE=3����GDE=60�㣬BC��DE��ͬһ��ֱ���ϣ��ҵ�C���D�غϣ��ֽ���ABC��D��E�ķ�����ÿ��1����λ���ٶ������˶�������B���E�غ�ʱֹͣ����������˶������У���ABC���ı���DEFG���غϲ��ֵ����S���˶�ʱ��t֮��ĺ�����ϵͼ������ǣ� ��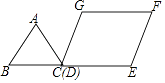
A.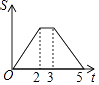
B.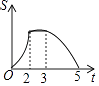
C.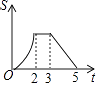
D.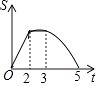
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com