解:(1)是;
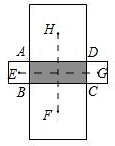
连接EG,FH,

∵E,F,G,H分别是四个正方形对角线的交点,
∴EG与FH平分、垂直且相等,
∴四边形EFGH 是正方形;
(2)能;
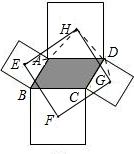
连接EG,FH,
∵E,F,G,H分别是四个正方形对角线的交点,
∴EG与FH平分,EG=FH,EG⊥FH,
∴四边形EFGH 是正方形;
(3)证明:连接EF、FG、GH、HE、AE、AH、DG、DH,
∵四边形ABCD是平行四边形,
∴AB=CD,
即以ABCD为边的正方形的对角线也相等,
∵点E、G是上述两个正方形的对角线的交点,
∴AH=DH,
易知∠HDG=∠HDA+∠ADC+∠CDG+45°=90°+∠ADC,
∵平行四边形ABCD中,有∠BAD=180°-∠ADC,
∴∠HAE=360°-(∠HAD+∠BAD+∠BAE)=360°-[45°+(180°-∠ADC)+45°]=90°+∠ADC,
∴∠HDG=∠HAE,
∴△HDG≌△HAE,
∴HG=HE且∠EHA=∠GHD,
同理可证HE=EF=FG,
∴四边形EFGH是菱形,
∵点H是正方形的对角线的交点,
∴∠AHD=90°,即∠AHG+∠GHD=90°,
∴∠EHG=90°,
∴四边形EFGH是正方形.
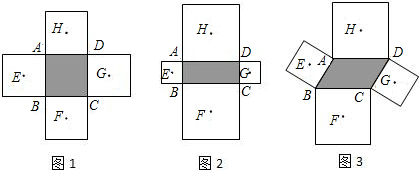
分析:(1)(2)连接EG,FH,可证明EG与FH平分垂直且相等;
(3)连接EF、FG、GH、HE、AE、AH、DG、DH,由四边形ABCD是平行四边形,得AH=DH,再证明△HDG≌△HAE,则HG=HE且∠EHA=∠GHD,同理可证HE=EF=FG,即可得出四边形EFGH是菱形.又因为点H是正方形的对角线的交点,则∠EHG=90°,即可证明四边形EFGH是正方形.
点评:本题考查了正方形的性质、全等三角形的判定以及平行四边形、矩形的性质,是一道综合性的题目,难度不大,要熟练掌握.






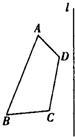 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.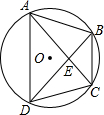 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
