
 如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.
如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°. 分析 根据角平分线的定义和三角形的外角的性质即可得到∠D=$\frac{1}{2}$∠A,代入求出即可.
解答 解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,
∴∠1=$\frac{1}{2}$∠ACE,∠2=$\frac{1}{2}$∠ABC,
又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,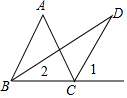
∴∠D=$\frac{1}{2}$∠A,
∵∠BDC=25°,
∴∠A=50°,
∵AB=AC,
∴∠ABC=$\frac{180°-50°}{2}$=65°,
故答案为:65°.
点评 此题综合考查了三角形的外角的性质以及角平分线定义的应用,解此题的关键是求出∠D=$\frac{1}{2}$∠A,难度适中.


科目:初中数学 来源: 题型:解答题
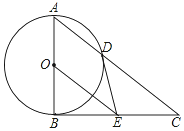 如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
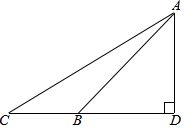 如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
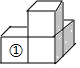 如图,是由4个同样大小的正方体摆成的几何体,将正方体①移走后,关于所得几何体的视图叙述正确的是( )
如图,是由4个同样大小的正方体摆成的几何体,将正方体①移走后,关于所得几何体的视图叙述正确的是( )| A. | 左视图改变 | B. | 主视图不变 | C. | 俯视图改变 | D. | 三视图都不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
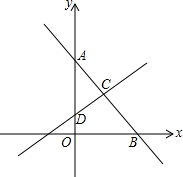 如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.
如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形BCFG,点P是DF的中点.若OP=6$\sqrt{2}$,AB=10,则△ABC的面积=( )
如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形BCFG,点P是DF的中点.若OP=6$\sqrt{2}$,AB=10,则△ABC的面积=( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com