
分析 (1)欲证明无论a为何值,该抛物线与x轴总有两个交点,只要证明△>0即可;
(2)对于抛物线y=ax2-3ax-4a(a<0),令y=0,ax2-3ax-4a=0,解得x=-1或4,推出A(-1,0),B(4,0),令x=0,y=-4a,推出C(0,-4a),由题意$\frac{1}{2}$•5•(-4a)=7.5,求出a即可解决问题;
(3)如图,假设存在,MD=3DP,设DP=m,则DM=3m,PM=2m.由△EDP≌△PMF,推出DE=PM=2m,易知NM=m,可得D($\frac{3}{2}$+m,3m),把点D($\frac{3}{2}$+m,3m)代入y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.得到3m=-$\frac{3}{4}$($\frac{3}{2}$+m)2+$\frac{9}{4}$($\frac{3}{2}$+m)+3,解方程即可解决问题;
解答 解:(1)对于抛物线y=ax2-3ax-4a(a<0),
∵△=(-3a)2-4•a•(-4a)=9a2+16a2=25a2,
∵a<0,
∴△>0,
∴无论a为何值,该抛物线与x轴总有两个交点.
(2)对于抛物线y=ax2-3ax-4a(a<0),
令y=0,ax2-3ax-4a=0,解得x=-1或4,
∴A(-1,0),B(4,0),
令x=0,y=-4a,
∴C(0,-4a),
由题意$\frac{1}{2}$•5•(-4a)=7.5,
∴a=-$\frac{3}{4}$,
∴此抛物线的解析式y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.
(3)如图,假设存在,MD=3DP,设DP=m,则DM=3m,PM=2m.
∵PE=PF,
∵PE⊥PF,
∴∠EPF=90°,
∴∠EPD+∠FPM=90°,
∵∠EPD+∠PED=90°,
∴∠PED=∠FPM,∵∠EDP=∠PMF,
∴△EDP≌△PMF,
∴DE=PM=2m,易知NM=m,
∴D($\frac{3}{2}$+m,3m),把点D($\frac{3}{2}$+m,3m)代入y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.
∴3m=-$\frac{3}{4}$($\frac{3}{2}$+m)2+$\frac{9}{4}$($\frac{3}{2}$+m)+3,
解得m=$\frac{-3+\sqrt{41}}{2}$或$\frac{-3-\sqrt{41}}{2}$(舍弃),
∴D($\frac{\sqrt{41}}{2}$,$\frac{-9+3\sqrt{41}}{2}$).
点评 本题考查二次函数综合题、待定系数法、全等三角形的判定和性质等知识,解题的关键是学会构建方程解决问题,学会利用参数解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.
如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 0 | C. | 2 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.
已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
| 社会消费品零售总额(单位:亿元) | 7702.8 | 8375.1 | 9098.1 | 10338 | 11005.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
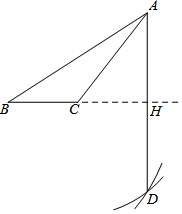 如图,已知钝角△ABC,老师按照如下步骤尺规作图:
如图,已知钝角△ABC,老师按照如下步骤尺规作图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 画线段AB=2 cm | B. | 画射线AB=3cm | ||
| C. | 在射线AC上截取AB=3cm | D. | 延长线段AB到点C,使得AC=2AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 合理的 | B. | 不能确定 | C. | 不合理的 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com