

图11-2-11
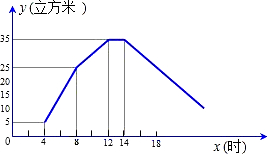
(1)求每小时的进水量;?(2)当8≤x≤12时,求y与x的函数关系式;?(3)当14≤x≤18时,求y与x的函数关系式.
|
思路解析:(1)由4点到8点(4个小时)共进水20立方米,从而可求出1小时的进水量.(2)因线段过点(8,25)和(12,35),可用待定系数法求其解析式.
(3)从图象上可以看出:所求函数过点(14,35),由(2)得每小时出水量为2.5立方米,从而可求得当x=16时,y=30,于是不难求出此函数解析式.解:(1)由图象可知,4点到8点进水20立方米,∴每小时进水量为5立方米.(2)当8≤x≤12时,由图知,线段过点(8,25)和(12,35),设函数解析式为y=kx+b, 则 ∴当8≤x≤12时,y与x的函数关系式为y=2.5x+5.(3)由(2)得,每小时出水量为2.5立方米,所以x=16时,y=30,设14≤x≤18时,函数解析式为y=mx+n, 则 ∴当14≤x≤18时,y与x的函数关系式为y=-2.5x+70. |


科目:初中数学 来源: 题型:
 方米)与时间x(时)的函数关系如图所示.
方米)与时间x(时)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源:新教材新学案 数学 八年级上册 题型:013
某贮水塔在工作期间每小时的进水量和出水量都是固定不变的.某日从凌晨4点到8点只进水不出水;8点到12点既进水又出水;14点至次日凌晨只出水不进水(如图所示).则水塔内贮水量为30方米的时间段为

A.0~4时
B.4~8时
C.8~12时
D.12~14时
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《一次函数》(03)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年山西省太原市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com