
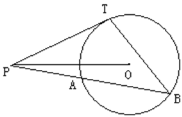
【题目】已知:如图,点P是半径为5cm的⊙O外的一点,OP= 13cm,PT切⊙O于T点,过点P作PB(PB>PA),设PA= x,PB= y。
(1)求y与x的函数解析式,并确定自变量x的取值范围;
(2)这个函数有最大值吗?若有求出此时△PBT的面积,若没有,请说明理由;
(3)是否存在这样的PB,使得![]() ,若存在,请求出PA的值,若不存在,请说明理由.
,若存在,请求出PA的值,若不存在,请说明理由.
【答案】(1)y=![]() (8<x<12);(2)有最大值,当PAB与PO重合时y最大, y最大=18, 这时
(8<x<12);(2)有最大值,当PAB与PO重合时y最大, y最大=18, 这时![]() ;
;
(3)存在这样的PB,A是PB的中点,这时,PA=x=6![]() .
.
【解析】
(1)连接圆心和切线,求得切线长,利用切割线定理可求得y关于x的函数解析式;(2)根据自变量的取值,求得函数的最值,进而求得面积;(3)利用三角形相似的面积求得相应的对应边的长.
(1)连接OT,∵PT切⊙O于T点,
∴∠OTP=90°,
∵OP=13cm,OT=5cm,
∴PT=12,
∵PT为切线,
∴PT2=PA×PB
∴xy=144,
∴y=![]() (8<x<12);
(8<x<12);
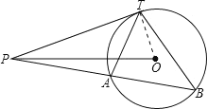
(2)由(1)得x=8时,y最大=18,此时TB为直径,TB=10,
∴S△PBT=![]()
(3)∵∠TPA=∠TPA, ∠PTA=∠PBT,
∴△PTA∽△PBT
∵![]()
∴PA:PT=1:![]()
∵PT=12,
∴PA=6![]()
∵在自变量的取值范围内,故存在.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
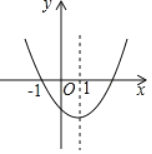
【题目】如图,是二次函数y=ax2+bx+c的图象,下列结论:①abc>0;②2a+b<0;③![]() <1,④a+c>0,其中正确的结论为_____(请把正确结论的序号都填在横线上)
<1,④a+c>0,其中正确的结论为_____(请把正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
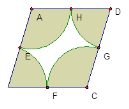
【题目】如图,菱形ABCD,边长等于2,点E、F、G、H分别是AB、BC、CD、DA的中点,图中阴影部分由四个小扇形组成,对于下列判断中正确的有( )
①空白图形空白部分的周长=2![]() ②空白部分的面积=
②空白部分的面积=![]()
③四个小扇形的面积和 =![]() ④菱形的面积=4
④菱形的面积=4
A 1个 B 2个 C 3个 D 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
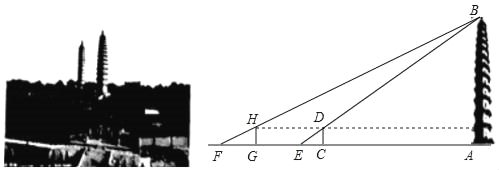
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
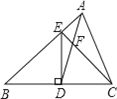
【题目】已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,同学们的学习习惯也有了改变,一些同学在做题遇到困难时,喜欢上网查找答案.针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图.
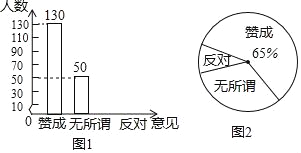
请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生?
(2)将图1补充完整;
(3)求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校1500名学生中有多少名学生持“无所谓”意见.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com