练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．底角为45°的等腰三角形一边长为4cm，则此等腰三角形的底边长=4或$4\sqrt{2}$cm．

    分析 由于长为4cm的边可能为腰，也可能为底边，故应分两种情况讨论．

    解答 解：由题意知，底角为45°的等腰三角形是等腰直角三角形，应分两种情况：
    （1）当腰长为4cm时，则另一腰也为4cm
    底边为4$\sqrt{2}$，
    （2）当底边长为4cm时．
    故答案为：4或$4\sqrt{2}$

    点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

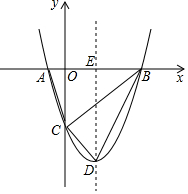    14．如图，抛物线与x轴交于A，B两点，点B坐标是（3，0），与y轴交于点C，顶点D的坐标是（1，-4），对称轴与x轴交于点E
    （1）求抛物线的解析式；
    （2）判断△AOC与△BCD是否相似？并证明你的结论；
    （3）在对称轴右侧上找点M，过点M作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知在四边形ABCD中，∠A=90°，AB=3，AD=4，BC=12，CD=13，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

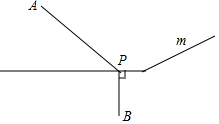    18．如图所示，在两个村庄A，B附近的河流可以近似地看成一条折线段（图中m）A，B分别在河的两旁，现要在河边修一个水泵站，同时向A，B两村供水，为了节约建设的费用，就要使所铺设的管道最短，某人甲提出了这样的建议：从点B向河道作垂线交m于点P，则点P为水泵站的位置．
    （1）你认为甲的建议符合要求吗？（管道总长最短）
    （2）若认为合理，请说明理由，若不认同，那么你认为水泵站应该建在哪里？请在图中标出来，并说明作图的依据．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴、y轴的正半轴上，OA=4，OC=2，点P从点O出发，沿x轴以每秒1个单位的速度向点A匀速运动，到达点A时停止运动，设点P运动的时间是t秒（t＞0），过点P作∠DPA=∠CPO，且PD=$\frac{1}{2}$CP，连接DA．
    （1）点D的坐标为（$\frac{3}{2}$t，1）．（请用含t的代数式表示）
    （2）点P在从点O向点A运动的过程中，△DPA能否成为直角三角形？若能，求t的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

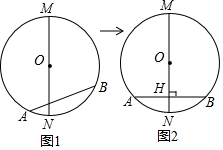
    15．在进行垂径定理的证明教学中，老师设计了如下活动：先让同学们在圆中作了一条直径MN，然后任意作了一条弦（非直径），如图1，接下来老师提出问题：在保证弦AB长度不变的情况下，如何能找到它的中点？
    在同学们思考作图验证后，小华说了自己的一种想法：只要将弦AB与直径MN保持垂直关系，如图2，它们的交点就是弦AB的中点．请你说出小华此想法的依据是等腰三角形三线合一定理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

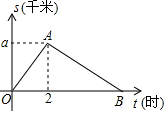    2．平顶山市教育局举行'重走长征路”健步活动，某教师从起点体育村沿建设路到市生态园．再沿原路返回．该教师离开起点的路程S（千米）与步行时间t（小时）之间的函数关系如图所示．其中从起点到市生态园的平均速度是4千米/小时．用2小时．根据图象提供信息．解答下列问题
    （1）求图中的a的值．
    （2）若在距离起点5千米处有一个地点C，该教师从第一次经过点C到第二次经过点C，所用时间为1.75小时
    ①求AB所在直线的函数关系式；
    ②该教师走完全程用多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知a=-1，b=2，求代数式5（2a2b-ab2）-4（ab2+3a2b）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：
    （1）8+（-10）-（-5）+（-2）
    （2）（-2）3-（1-$\frac{1}{3}$）×（1-4）

    查看答案和解析>>

    同步练习册答案