
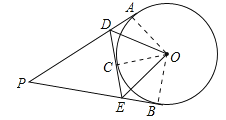
【题目】如图,PA,PB,DE切⊙O于点A,B,C,D在PA上,E在PB上,
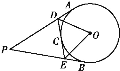
(1)若PA=10,求△PDE的周长;
(2)若∠P=50°,求∠O的度数.
【答案】(1)20;(2)65°.
【解析】试题(1)于PA、PB、DE都是⊙O的切线,可由切线长定理将切线PA、PB的长转化为△PDE的周长;
(2)连接OA、OC、0B,利用切线长定理即可得到∠O=![]() ∠AOB,由四边形的内角和可得∠AOB+∠P=180°,进而求出∠O的度数.
∠AOB,由四边形的内角和可得∠AOB+∠P=180°,进而求出∠O的度数.
试题解析:解:(1)∵PA、PB、DE分别切⊙O于A、B、C,∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20;∴△PDE的周长为20;
(2)连接OA、OC、0B,∵OA⊥PA,OB⊥PB,OC⊥DE,∴∠DAO=∠EBO=90°,∴∠P+∠AOB=180°,∴∠AOB=180°﹣50°=130°,∵∠AOD=∠DOC,∠COE=∠BOE,∴∠DOE=![]() ∠AOB=
∠AOB=![]() ×130°=65°.
×130°=65°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.
如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27
(1)求(﹣4)☆7的值;
(2)若(1﹣3x)☆(﹣4)=32,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
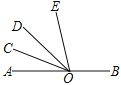
【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为___________.(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点.
(1)如图2,数轴上点A、B表示的数分别为-4、12,点D是线段AB的三等分点,求点D在数轴上所表示的数;
(2)在(1)的条件下,点P从点A出发以每秒1个单位长度的速度在数轴上向右运动;点Q从点B出发,在数轴上先向左运动,与点P重合后立刻改变方向与点P同向而行,且速度始终为每秒3个单位长度,点P、Q同时出发,设运动时间为t秒.
①用含t的式子表示线段AQ的长度;
②当点P是线段AQ的三等分点时,求点P在数轴上所表示的数.
![]()
图1

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一点A(4,-1),将点A向左平移5个单位再向上平移5个单位得到点B,直线![]() 过点A、B,交x轴于点C,交y轴于点D, P是直线上的一个动点,通过研究发现直线
过点A、B,交x轴于点C,交y轴于点D, P是直线上的一个动点,通过研究发现直线![]() 上所有点的横坐标x与纵坐标y 都是二元一次方程x+y=3的解.
上所有点的横坐标x与纵坐标y 都是二元一次方程x+y=3的解.
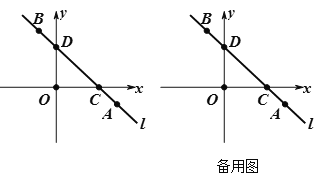
①直接写出点B,C,D的坐标;B_______, C_________, D________
②求![]()
③当![]() 时,求点P的坐标.
时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.这里的右图,是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30CM、宽20CM、高18CM,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
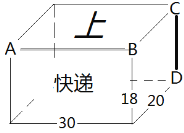
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30CM、宽20CM、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东行驶了![]() 千米到达小彬家,继续向东行驶了
千米到达小彬家,继续向东行驶了![]() 千米到达小颖家,然后向西行驶了
千米到达小颖家,然后向西行驶了![]() 千米到达小明家,最后回到超市.
千米到达小明家,最后回到超市.
(1)以超市为原点,向东为正,以![]() 个单位长度表示
个单位长度表示![]() ,在数轴上表示出上述各地点的位置.
,在数轴上表示出上述各地点的位置.
(2)请列式计算小明家在超市什么方向?距超市多远?
(3)若货车每千米油耗![]() 升,这辆货车共耗油多少升?
升,这辆货车共耗油多少升?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com