
【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
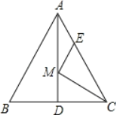
【答案】![]()
【解析】试题分析:要求EM+CM的最小值,需考虑通过作辅助线转化EM,CM的值,从而找出其最小值求解.
解:连接BE,与AD交于点M.则BE就是EM+CM的最小值.
取CE中点F,连接DF.
∵等边△ABC的边长为6,AE=2,
∴CE=AC﹣AE=6﹣2=4,
∴CF=EF=AE=2,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,
∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE﹣ME=4ME﹣ME=3ME,
∴BE=BM.
在直角△BDM中,BD=BC=3,DM=AD=![]() ,
,
∴BM=![]() =
=![]() ,
,
∴BE=![]() .
.
∵EM+CM=BE
∴EM+CM的最小值为.
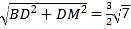


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,0),B(0,3),以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P![]() ,且△ABP的面积与△ABC的面积相等.
,且△ABP的面积与△ABC的面积相等.
(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在一点M,使△MAC为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价15%后的售价为1.15元,则该商品在甲商场的原价为 ▲ 元;
(2)乙商场将该商品提价20%后,用6元钱购买该商品的件数比没提价前少买1件,求该商品在乙商场的原价是多少?
(3)在(1)、(2)小题的条件下,甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是![]() ,第二次提价的百分率是
,第二次提价的百分率是![]() ;
;
乙商场:两次提价的百分率都是![]() (
(![]() .
.
请问甲、乙两商场,哪个商场的提价较多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列计算过程,发现规律,利用规律猜想并计算:
1+2=![]() =3;1+2+3=
=3;1+2+3=![]() =6,1+2+3+4=
=6,1+2+3+4=![]() =10;1+2+3+4+5=
=10;1+2+3+4+5=![]() =15;…
=15;…
(1)猜想:1+2+3+4+…+n= .
(2)利用上述规律计算:1+2+3+4+…+200;
(3)尝试计算:3+6+9+12+…3n的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:G):
492,496,494,495,498,497,501,502,504,496
497,503,506,508,507,492,496,500,501,499
根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概率为( )
A.![]() B
B ![]() C
C ![]()
B.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2015年12月月历.
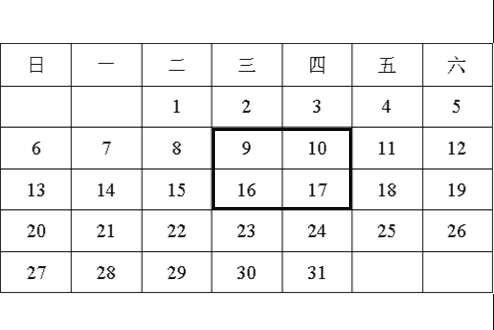
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.
(2)帮助小智求出⊙O的直径 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
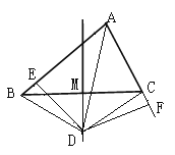
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
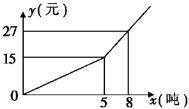
【题目】某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,
(1)分别写出x≤5和x>5的函数解析式;
(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;
(3)若某户居民六月交水费31元,则用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com