
【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为cm. 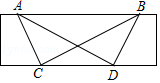
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 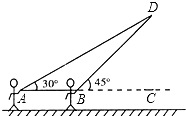
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化简:4A﹣(2B+3A),将结果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值与字母 x 的取值无关,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=![]() ,即1+3+32+33+…+3100=
,即1+3+32+33+…+3100=![]() .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.
(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=x与双曲线y= ![]() 相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点. 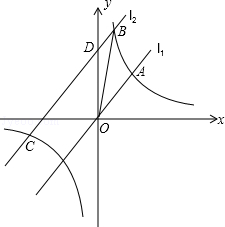
(1)求双曲线y= ![]() 的解析式;
的解析式;
(2)求tan∠DOB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).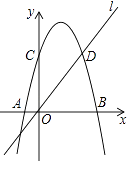
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com