
分析 (1)设乙工程队每天能完成绿化的面积是xm2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
(2)用总工作量减去甲队的工作量,然后除以乙队的工作效率即可求解;
(3)设甲队施工n天,由(2)知乙队施工(20-2n)天,令施工总费用为w万元,求出w与n的函数解析式,根据n的取值范围以及一次函数的性质求解即可.
解答 解:(1)设乙工程队每天能完成绿化的面积是xm2,则甲工程队每天能完成绿化的面积是2xm2,
根据题意得:$\frac{200}{x}$-$\frac{200}{2x}$=2,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)甲队完成的绿化面积:100n m2,
剩余的绿化面积:(1000-100n)m2,
乙队施工的天数:$\frac{1000-100n}{50}$=20-2n;
(3)设甲队施工n天,由(2)知乙队施工(20-2n)天,令施工总费用为w万元,
则w=0.6n+0.25(20-2n)=0.1n+5.
∵两队施工的天数之和不超过15天,
∴n+(20-2n)≤15,
∴n≥5,
∴当n=5时,w有最小值5.5万元,此时甲队施工5天,乙队施工10天.
答:安排甲队施工5天,乙队施工10天,可使施工总费用最低,最低费用为5.5万元.
点评 本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
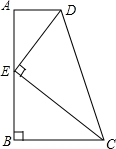 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )| A. | CE=$\sqrt{3}$DE | B. | CE=$\sqrt{2}$DE | C. | CE=3DE | D. | CE=2DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
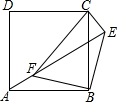 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
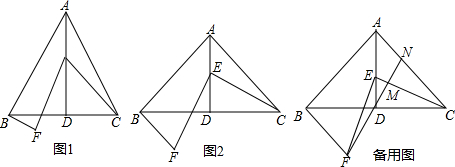
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数形结合 | B. | 换元与降次 | C. | 消元 | D. | 公理化 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com