
【题目】通过计算我们知道:
(a-1)(a+1)=a2-1
(a-1)(a2+a+1)=a3-1
(a-1)(a3+a2+a+1)=a4-1
(1)请根据以上计算规律填空:(a-1)(an+an-1+…+a3+a2+a+1)=______
(2)根据上述规律,请你求出32018+32017+…+33+32+3+1的个位上的数字.
【答案】(1)an+1-1;(2)![]() (32019-1)
(32019-1)
【解析】
(1)通过计算先找到规律,根据规律得结论;
(2)先把32018+32017+…+33+32+3+1乘以![]() (3-1)变形为(1)中规律的形式,计算出结果.再找到3n的个位数字变化规律,得结论.
(3-1)变形为(1)中规律的形式,计算出结果.再找到3n的个位数字变化规律,得结论.
解:(1)由以上计算规律可知:
(a-1)(an+an-1+…+a3+a2+a+1)=an+1-1,
故答案为:an+1-1;
(2)32018+32017+…+33+32+3+1
=![]() (3-1)(32018+32017+…+33+32+3+1)
(3-1)(32018+32017+…+33+32+3+1)
=![]() (32019-1)
(32019-1)
因为31=3,32=9,33=27,34=81,
35的个位数字为3,36的个位数字为9,37的个位数字为7,38的个位数字为1…
所以32019的个位数字是7,
所以原式的个位数字是3.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个车队共有20辆小轿车,正以每小时36千米的速度在一条笔直的街道上匀速行驶,行驶时车与车的间隔均相等,甲停在路边等人,他发现该车队从第一辆车的车头到最后一辆的车尾经过自己身边共用了20秒的时间,假设每辆车的车长均为4.87米.
(1)求行驶时车与车的间隔为多少米?
(2)若乙在街道一侧的人行道上与车队同向而行,速度为![]() 米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求
米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.

(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数。例如:M{1,0,2}=![]() ;min{1,0,2}=1;min{1,0,a}=
;min{1,0,2}=1;min{1,0,a}=![]() .如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
.如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,∠C=50°,E是BA延长线上的一点,过点A作![]() //BC﹒若AD平分∠CAE,求∠B的度数.
//BC﹒若AD平分∠CAE,求∠B的度数.

解:∵![]() //BC,∠C=50°( 已知 ),
//BC,∠C=50°( 已知 ),
∴∠2= = °( ).
又∵AD平分∠CAE( 已知 ),
∴ =∠2=50°( ).
又∵![]() //BC(已知),
//BC(已知),
∴∠B= = °( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.

(1)问题的结论:DF______AE.
(2)证明思路欲证DF______AE,只要证∠3=______.
(3)证明过程:
证明:∵CD⊥DA,DA⊥AB,( )
∴∠CDA=∠DAB=______°(垂直定义)
∵∠1=∠2,( )
∴∠CDA-∠1=______-______,(等式的性质)
即∠3=______
∴DF______AE( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
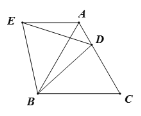
【题目】如图,在等边 ABC中,D是边AC上一点,连接BD. 将 BCD绕点B逆时针旋转60°得到 BAE,连接ED. 若BC=10,BD=9,求 AED的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com