
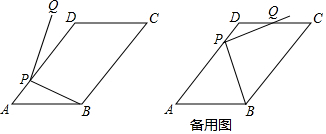
分析 (1)分两种情形①当点Q在平行四边形ABCD内时,②当点Q在平行四边形ABCD外时,分别求解即可;
(2)如图2中,连接BQ,作PE⊥AB于E.在Rt△APE中,tanA=$\frac{PE}{AE}$=$\frac{4}{3}$,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP=$\frac{PE}{EB}$=2,推出EB=2k,推出AB=5k=10,可得k=2,由此即可解决问题;
(3)分三种情形分别求解即可;
解答 解:(1)如图1中,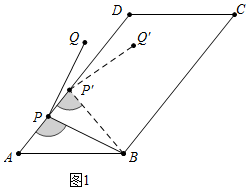
①当点Q在平行四边形ABCD内时,∠AP′B=180°-∠Q′P′B-∠Q′P′D=180°-90°-10°=80°,
②当点Q在平行四边形ABCD外时,∠APB=180°-(∠QPB-∠QPD)=180°-(90°-10°)=100°,
综上所述,当∠DPQ=10°时,∠APB的值为80°或100°.
(2)如图2中,连接BQ,作PE⊥AB于E.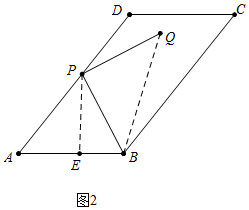
∵tan∠ABP:tanA=3:2,tanA=$\frac{4}{3}$,
∴tan∠ABP=2,
在Rt△APE中,tanA=$\frac{PE}{AE}$=$\frac{4}{3}$,设PE=4k,则AE=3k,
在Rt△PBE中,tan∠ABP=$\frac{PE}{EB}$=2,
∴EB=2k,
∴AB=5k=10,
∴k=2,
∴PE=8,EB=4,
∴PB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∵△BPQ是等腰直角三角形,
∴BQ=$\sqrt{2}$PB=4$\sqrt{10}$.
(3)①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F.则四边形BEPF是矩形.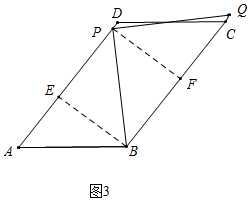
在Rt△AEB中,∵tanA=$\frac{BE}{AE}$=$\frac{4}{3}$,∵AB=10,
∴BE=8,AE=6,
∴PF=BE=8,
∵△BPQ是等腰直角三角形,PF⊥BQ,
∴PF=BF=FQ=8,
∴PB=PQ=8$\sqrt{2}$,
∴PB旋转到PQ所扫过的面积=$\frac{90•π•(8\sqrt{2})^{2}}{360}$=32π.
②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F.设PE=x.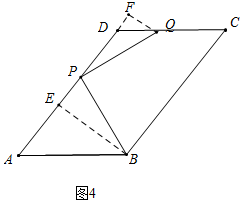
易证△PBE≌△QPF,
∴PE=QF=x,EB=PF=8,
∴DF=AE+PE+PF-AD=x-1,
∵CD∥AB,
∴∠FDQ=∠A,
∴tan∠FDQ=tanA=$\frac{4}{3}$=$\frac{FQ}{DF}$,
∴$\frac{x}{x-1}$=$\frac{4}{3}$,
∴x=4,
∴PE=4,$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
在Rt△PEB中,PB=,$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴PB旋转到PQ所扫过的面积=$\frac{90•π•(4\sqrt{5})^{2}}{360}$=20π
③如图5中,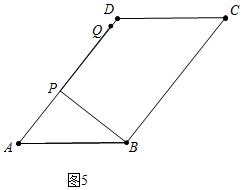
当点Q落在AD上时,易知PB=PQ=8,
∴PB旋转到PQ所扫过的面积=$\frac{90•π•{8}^{2}}{360}$=16π,
综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π.
点评 本题考查四边形综合题、平行四边形的性质、全等三角形的判定和性质、锐角三角函数、勾股定理、扇形的面积公式等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
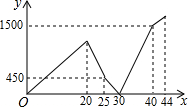 小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.
小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b≥-1 | B. | b≤-1 | C. | b≥-2 | D. | b≤-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
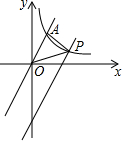 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,则k=2;△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,则k=2;△POA的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
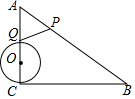 如图,Rt△ACB中,∠C=90°,AC=3,BC=4,半径为1的⊙O,圆心O在AC上且与BC相切,P是线段AB上的动点,过点P作⊙O的一条切线PQ,Q为切点,则PQ的最小值为$\frac{\sqrt{39}}{5}$.
如图,Rt△ACB中,∠C=90°,AC=3,BC=4,半径为1的⊙O,圆心O在AC上且与BC相切,P是线段AB上的动点,过点P作⊙O的一条切线PQ,Q为切点,则PQ的最小值为$\frac{\sqrt{39}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
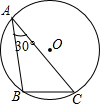 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2\sqrt{3}π}{3}$ | D. | $\frac{\sqrt{3}π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com