
【题目】如图,抛物线y= ![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
【答案】
(1)解:把点A(0,﹣6)、B(﹣2,0)代入抛物线y= ![]() x2+bx+c中得:
x2+bx+c中得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y= ![]() x2﹣2x﹣6;
x2﹣2x﹣6;
(2)解:y= ![]() x2﹣2x﹣6,
x2﹣2x﹣6,
当y=0时, ![]() x2﹣2x﹣6=0,
x2﹣2x﹣6=0,
解得:x1=﹣2,x2=6,
∴C(6,0);
设直线AC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]() ,
,
∴直线AC的解析式为:y=x﹣6,
直线AC向下平移m个单位后的直线关系式为:y=x﹣6﹣m,
∵平移后的直线与抛物线有且只有一个公共点M,
则 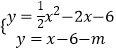 ,
,
得: ![]() =0,
=0,
△=(﹣3)2﹣4× ![]() m=0,
m=0,
m= ![]() ,
,
代入得:y=x﹣6﹣m=x﹣ ![]() ,
,
则 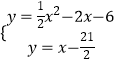 ,
,
解得: 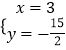 ,
,
∴M(3,﹣ ![]() );
);
(3)解:分三种情况:
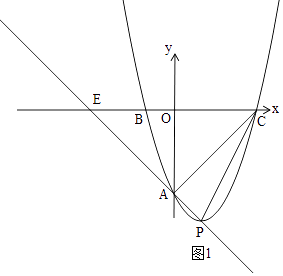
①当∠PAC=90°时,如图1,
∵OA=OC=6,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∴△EAC是等腰直角三角形,
∴AE=AC,
∴OE=OC=6,
∴E(﹣6,0),
设AE:y=kx+b,
则 ![]() ,解得:
,解得: ![]() ,
,
∴直线AE的解析式为:y=﹣x﹣6,
则 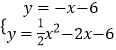 ,
,
![]() ﹣2x﹣6=﹣x﹣6,
﹣2x﹣6=﹣x﹣6,
解得:x1=0(舍),x2=2,
∴P(2,﹣8),
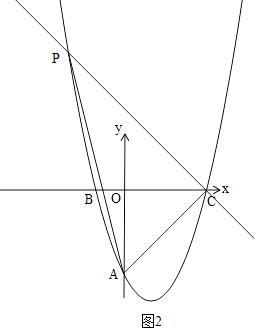
②当∠ACP=90°时,如图2,
∠PCB=90°﹣45°=45°,
过P作PE⊥BC于E,
∴△PEC是等腰直角三角形,
∴PE=EC,
设P(x, ![]() x2﹣2x﹣6),
x2﹣2x﹣6),
∴PE= ![]() x2﹣2x﹣6,EC=﹣x﹣6,
x2﹣2x﹣6,EC=﹣x﹣6,
∴ ![]() x2﹣2x﹣6=﹣x﹣6,
x2﹣2x﹣6=﹣x﹣6,
解得:x1=6,x2=﹣4,
∵P在第二象限,
∴x=6不符合题意,舍去,x=﹣4,
∴P(﹣4,10),
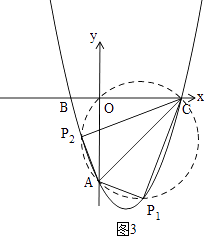
③以AC为直径画圆,交抛物线于两点P1、P2,如图3,
则∠AP1C=∠AP2C=90°,
∵ ![]() =
= ![]() ,
,
![]() =
= ![]() ,
,
AC2=62+62=72,
由勾股定理得: ![]() +
+ ![]() =72,
=72,
化简得:x3﹣8x2+8x+24=0,
x3﹣2x2﹣4x﹣(6x2﹣12x﹣24)=0,
x(x2﹣2x﹣4)﹣6(x2﹣2x﹣4)=0,
(x﹣6)(x2﹣2x﹣4)=0,
解得:x1=6(舍),x2=1+ ![]() ,x3=1﹣
,x3=1﹣ ![]() ,
,
∴P(1+ ![]() ,﹣5﹣
,﹣5﹣ ![]() )或(1﹣
)或(1﹣ ![]() ,﹣5+
,﹣5+ ![]() ),
),
综上所述,△PAC为直角三角形时,点P的坐标为:(2,﹣8),(﹣4,10),(1+ ![]() ,﹣5﹣
,﹣5﹣ ![]() ),(1﹣
),(1﹣ ![]() ,﹣5+
,﹣5+ ![]() ).
).
【解析】(1)利用待定系数法求二次函数的解析式;(2)由直线向下平移m个单位得:y=x﹣6﹣m,由直线与抛物线有且只有一个公共点M可知:由解析式列方程组根据△=0,可得结论;(3)分三种情况:①当∠PAC=90°时,如图1,由△EAC是等腰直角三角形,可得E(﹣6,0),直线AP与抛物线的交点就是P,列方程组可得P的坐标;②当∠ACP=90°时,如图2,由PE=EC,列式: ![]() x2﹣2x﹣6=﹣x﹣6,解出即可;③当APC=90°时,如图3,画圆,根据直径所对的圆周角是直角可知,有两个点符合,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标.
x2﹣2x﹣6=﹣x﹣6,解出即可;③当APC=90°时,如图3,画圆,根据直径所对的圆周角是直角可知,有两个点符合,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标.


科目:初中数学 来源: 题型:
【题目】如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数. ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请观察下列算式,找出规律并填空
①![]() =1﹣
=1﹣![]() ,②
,②![]() =
=![]() ×(1﹣
×(1﹣![]() ),③
),③![]() =
=![]() ×(1﹣
×(1﹣![]() ),④
),④![]() =
=![]() ×(1﹣
×(1﹣![]() ),…
),…
(1)则第10个算式是______,
(2)第n个算式为_______=_______.
(3)从以上规律中你可得到一些启示吗?根据你得到的启示,试解答下题:
若有理数a、b满足|a﹣1|+(b﹣3)2=0,
求![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
(4)如图,把一个面积为1的正方形等分成两个面积为![]() 的长方形,接着把面积为
的长方形,接着把面积为![]() 的长方形等分成两个面积为
的长方形等分成两个面积为![]() 的正方形,再把面积为
的正方形,再把面积为![]() 的正方形等分成两个面积为
的正方形等分成两个面积为![]() 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() (直接写答案)
(直接写答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
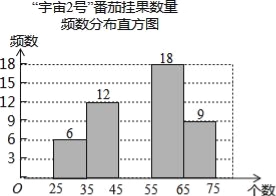
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
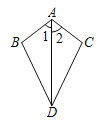
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com