
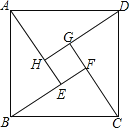
【题目】勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
地,约定向东为正方向,当天的航行路程记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)请你帮忙确定![]() 地位于
地位于![]() 地的什么方向,距离
地的什么方向,距离![]() 地多少千米?
地多少千米?
(2)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求冲锋舟当天救灾过程中至少还需补充多少升油?
升,求冲锋舟当天救灾过程中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解重庆市的空气质量情况,我校初2017级“综合实践环境调查”小组从环境监测网随机抽取了若干天的空气质量作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出):
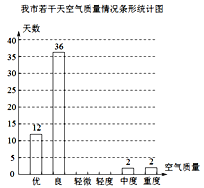
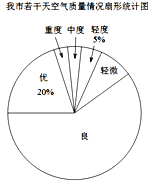
(1)课题小组随机抽取的天数为_______天,请将条形统计图补充完整;
(2)为找出优化环境的措施,“环境治理研讨小组”的同学欲从天气质量为“中度污染”和“重度污染”的样本中随机抽取两天分析污染原因,请用列表或画树状图的方法求出所抽取的两天恰好都是“重度污染”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
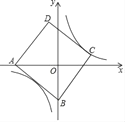
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.
【答案】![]()
【解析】解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°,∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE,∵点A的坐标为(﹣4,0),∴OA=4,∵AB=5,∴OB=![]() =3,在△ABO和△BCE中,∵∠OAB=∠CBE,∠AOB=∠BEC,AB=BC,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(3,1),∵反比例函数
=3,在△ABO和△BCE中,∵∠OAB=∠CBE,∠AOB=∠BEC,AB=BC,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(3,1),∵反比例函数![]() (k≠0)的图象过点C,∴k=xy=3×1=3,∴反比例函数的表达式为
(k≠0)的图象过点C,∴k=xy=3×1=3,∴反比例函数的表达式为![]() .故答案为:
.故答案为: ![]() .
.

点睛:本题考查的是反比例函数图象上点的坐标特点,涉及到正方形的性质,全等三角形的判定与性质,反比例函数图象上的点的坐标特征,作辅助线构造出全等三角形并求出点D的坐标是解题的关键.
【题型】填空题
【结束】
17
【题目】关于x的分式方程![]() =1的解是正数,则m的取值范围是_____.
=1的解是正数,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
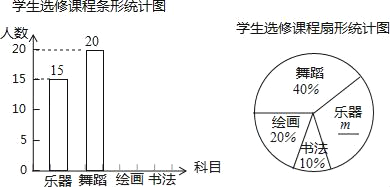
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
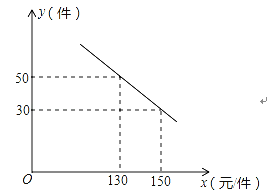
【题目】电商时代使得网购更加便捷和普及.小张响应国家号召,自主创业,开了家淘宝店.他购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
(1)求y与x之间的函数关系式;
(2)若某天小张销售该产品获得的利润为1200元,求销售单价x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M,N分别是AC,BC的中点.
![]()
(1)若AC=8 cm,CB=6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其他条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M,N分别为AC,BC的中点,你能猜想MN的长度吗?请画出图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com