



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解


查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 问题提出:如何把一个正方形分割成n(n≥9)个小正方形?
问题提出:如何把一个正方形分割成n(n≥9)个小正方形? (1)把一个正方形分割成9个小正方形.
(1)把一个正方形分割成9个小正方形.查看答案和解析>>
科目:初中数学 来源:山东省中考真题 题型:解答题
我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,把待解决的问题,通过某种转化过程,归结到一类已解决或比较容易解决的问题。
譬如,在学习了一元一次方程的解法以后,进一步研究二元一次方程组的解法时,我们通常采用“消元”的方法,把二元一次方程组转化为一元一次方程;再譬如,在学习了三角形内角和定理以后,进一步研究多边形的内角和问题时,我们通常借助添加辅助线,把多边形转化为三角形,从而解决问题。
问题提出:如何把一个正方形分割成n(n≥9)个小正方形?
为解决上面问题,我们先来研究两种简单的“基本分割法”,
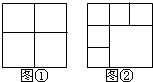
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形。
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com