
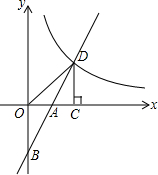
 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB≌△ACD.
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB≌△ACD.分析 (1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=$\frac{k}{x}$(x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-$\frac{b}{2}$,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系.
解答 解:(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=$\frac{k}{x}$(x>0)的图象上,
∴k=2×2=4;
(2)直线y=2x+b与坐标轴交点的坐标为A(-$\frac{b}{2}$,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=$\frac{k}{x}$(x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
点评 本题主要考查反比例函数与一次函数的交点问题,全等三角形的性质,解答本题的关键是熟练掌握反比例函数的性质以及反比例函数图象的特征,此题难度不大,是一道不错的中考试题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
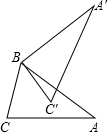 如图,在△ABC中,AB=AC,将△ABC绕B点逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′度数为( )
如图,在△ABC中,AB=AC,将△ABC绕B点逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
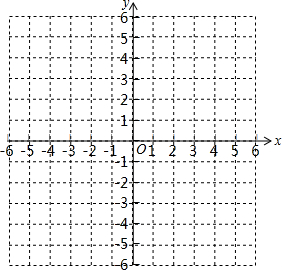 在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
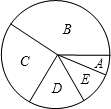 某校团委在寒假期间组织了以“合理安排时间,养成阅读习惯”为主题的教育活动,在学校随机调查了50名同学平均每天的阅读时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:
某校团委在寒假期间组织了以“合理安排时间,养成阅读习惯”为主题的教育活动,在学校随机调查了50名同学平均每天的阅读时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:| 组别 | 阅读的时间 | 频数 | 频率 |
| A | 1≤t<2 | 3 | 0.06 |
| B | 2≤t<4 | 20 | 0.40 |
| C | 4≤t<6 | m | 0.30 |
| D | 6≤t<8 | 8 | n |
| E | t≥8 | 4 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com