
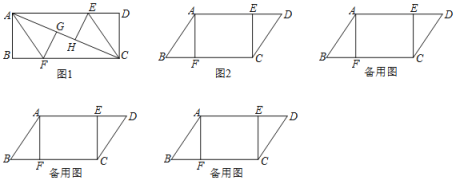
【题目】(1)如图1,长方形ABCD中分别沿AF、CE将AC两侧折叠,使点B、D分别落在AC上的G、H处,则线段AE______CF.(填“>”“<”或“=”)
(2)如图2,在平行四边形ABCD中,△ABF≌△CDE,AB=10cm,BF=6cm,AF=8cm,动点P、Q分别从A、C两点同时出发,点P自A→F→B→A停止,点Q自C→D→E→C停止.
①若点P的速度为每秒5cm,点Q的速度为每秒4cm,设运动时间为t秒.当点P在FB上运动,而点Q在DE上运动时,若四边形APCQ是平行四边形,求此时t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),利用备用图探究,当a与b满足什么数量关系时,四边形APCQ是平行四边形.
【答案】(1)=;(2)①![]() 秒;②a+b=24(ab≠0)
秒;②a+b=24(ab≠0)
【解析】
(1)根据内错角相等得出AF∥CE,由两对应边互相平行得出AFCE是平行四边形,即可得出AE=CF;
(2)①当P点在BF上,Q点在ED上时,能构成平行四边形,根据平行四边形的性质,列出方程求解即可;
②分三种情况:当点P在AF上,Q点在CE上时,AP=CQ;当点P在BF上,Q点在DE上时,AQ=CP;当点P在AB上,Q点在CD上时,AP=CQ,分别得出a与b满足的数量关系式.
解:(1)如图1,∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BAC=∠DCA,
由折叠的性质可知,∠FAC=![]() ∠BAC=
∠BAC=![]() ∠DCA=∠ECA,
∠DCA=∠ECA,
∴AF∥CE,
∴四边形AFCE是平行四边形,
∴AE=CF.
故答案为:=;
(2)①∵在平行四边形ABCD中,△ABF≌△CDE,
∴AE=CF,BF=DE=6cm,AB=CD=10cm,
∵如图2,当P点在BF上,Q点在ED上,以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
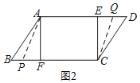
∴FP=EQ,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PF=5t-8,QE=16-4t,
∴5t-8=16-4t,
解得t=![]() ,
,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=![]() 秒;
秒;
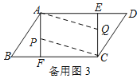
②由题意得,以A,C,P,Q四点的四边形是平行四边形时,点P、Q在相互平行的对边上,
分三种情况:
Ⅰ.如图3,当点P在AF上,Q点在CE上时,AP=CQ,
即a=24-b,得:a+b=24;
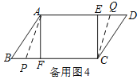
Ⅱ.如图4,当点P在BF上,Q点在DE上时,AQ=CP,
又∵AE=CF,
∴EQ=FP,
即16-b=a-8,得a+b=24;
Ⅲ.如图5,当点P在AB上,Q点在CD上时,AP=CQ,
即24-a=b,得a+b=24.
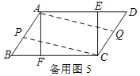
综上所述,a与b满足的数量关系式是a+b=24(ab≠0).


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是

A.①②③ B.①②④ C.②③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的对角线上任一点,PE⊥AB于E,PF⊥BC于F.
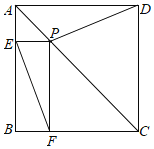
(1)判断DP与EF的关系,并证明;
(2)若正方形ABCD的边长为6,∠ADP:∠PDC=1:3.求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q也停止运动.设运动时间为ts,当t为何值时,以P,D,Q,B为顶点的四边形是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且![]() 于D,与⊙O交于点F.
于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com