练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知A=, B=2x2+4x+2.

    (1)化简A，并对B进行因式分解 

    (2)当B=0时,求A的值

    （1），2（x+1）2；（2）﹣2 【解析】试题分析：（1）先根据分式混合运算的法则把A进行化简，对B进行因式分解即可； （2）根据B=0求出x的值，代入A式进行计算即可． 试题解析：（1）A= = = = =； B=2x2+4x+2=2（x2+2x+1）=2（x+1）2； （2）∵B=0，∴2（x+1）2=0， ∴x=﹣1． 当x...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    解下列方程（不等式）组.

    (1)解方程组：

    (2) 解不等式组： ，并求其非负整数解.

    （1）（2）0，1, 2 【解析】试题分析：（1）方程①×3，然后利用加减消元法进行求解即可； （2）分别求出每一个不等式的解集，然后确定不等式组的解集，最后确定非负整数解即可. 试题解析：（1）， 由①×3+②，得： ， ， 把代入①得： ， ， 所以，原方程组的解为； （2）， 解不等式①，得： ， 解不等式②，得： ， 所以，不等式...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。

    （1）求证：AC是⊙O的切线；

    （2）若AD:DB=3:2，AC=15，求⊙O的直径。

    （1）连接OD、CD，先根据切线的性质得到OD⊥DE，即∠1+∠2=90°，再根据圆周角定理可得∠BDC=90°，再结合E为AC的中点，根据直角三角形的性质可得DE=CE=AE=AC，即得∠2=∠3，根据元的基本性质可得∠1=∠4，即得∠3+∠4=∠1+∠2=90°，从而证得结论；（2） 【解析】 试题分析：（1）连接OD、CD，先根据切线的性质得到OD⊥DE，即∠1+∠2=90°，再...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    在Rt△ABC中，∠C=900，∠B=2∠A，则cosB等于（ ）

    A. B. C. D.

    B 【解析】∵∠C=90°， ∴∠A+∠B=90°， ∵∠B=2∠A， ∴∠A+2∠A=90°， ∴∠A=30°， ∴∠B=60°， ∴cosB=. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    下面是最简二次根式的是（ ）

    A. B. C. D.

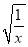    D 【解析】A选项： y，不是最简二次根式； B选项，不是最简二次根式； C选项： =，不是最简二次根式； D选项是最简二次根式. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型：填空题

    如图,将一根长24厘米的筷子,置于底面直径为6厘 米,高为8厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为_______厘米.

    14 【解析】试题解析：如图所示，筷子，圆柱的高，圆柱的直径正好构成直角三角形， ∴勾股定理求得圆柱形水杯的最大线段的长度，即=10cm， ∴筷子露在杯子外面的长度至少为24-10=14cm， 故答案为14．

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型：单选题

    若x+m与2-x的乘积中不含x的一次项,则实数m的值为( )

    A. -2 B. 2 C. 0 D. 1

    B 【解析】根据题意得： (x+m)(2?x)=2x?x2+2m?mx， ∵x+m与2?x的乘积中不含x的一次项， ∴m=2； 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

    （1）△BEF是等腰三角形吗？试说明理由；

    （2）若AB＝4，AD＝8，求CF的长度．

    见解析 【解析】试题分析：（1）由AD∥BC得到∠1=∠2，由折叠性质得到∠2=∠FEB，则∠1=∠FEB，于是可判断△EBF是等腰三角形； （2）设BE=x，则DE=x，AE=AD﹣DE=8﹣x，在Rt△ABE中，理由勾股定理得到（8﹣x）2+42=x2，解得x=5，而△EBF是等腰三角形，所以BF=BE=5，即可得到CF的长． 试题解析：【解析】 （1）△BEF是等腰三角形...

    查看答案和解析>>

    科目：初中数学 来源：贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    如图，已知数轴上点B表示的为-5，点A是数轴上一点，且AB=12，动点P从点A出发，以每秒1个单位长度的速度沿数轴向右匀速运动，动点H从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为（）秒．

    （1）写出数轴上点A表示的数　　　　　　；

    （2）当动点P，H同时从点A和点B出发，运动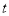秒时，点P表示的数 ；点H表示的数 ；（用含的代数式表示）

    （3）动点P、H同时出发，问点H运动多少秒时追上点P？

    （1）7；（2）7+t,2t-5;(3)12秒. 【解析】试题分析：（1）根据两点间距离公式可求出数轴上点A表示的数； （2）根据两点之间的距离公式可求点P表示的数与点H表示的数； （3）根据题意列出方程2t-5=7+ ， 求解即可. 试题解析：（1）∵数轴上点B表示的数为-5，A是数轴上一点，且AB=12， ∴AO=7， ∴数轴上点A表示的数为：7; （...

    查看答案和解析>>

    同步练习册答案