[题目]△ABC中.点O是AC边上一个动点.过点O作直线MN∥BC.设MN交∠BCA的平分线于E.交∠DCA的平分线于点F．(1)求证:EO＝FO,(2)当点O运动到何处时.四边形AECF是矩形?并证明你的结论．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠DCA的平分线于点F．

(1)求证：EO＝FO；

(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

【答案】略

【解析】

试题（1）由MN∥BC可得∠BCE=∠CEO，再结合∠BCE=∠ECO可得OE=OC，同理OC=OF，即可证得结论；

（2）先根据对角线互相平分的四边形的证得AECF为平行四边形，再根据CE、CF为△ABC内外角的平分线可得∠EOF=90°，即可证得结论.

（1）∵MN∥BC，

∴∠BCE=∠CEO

又∵∠BCE=∠ECO

∴∠OEC=∠OCE

∴OE=OC,同理OC=OF

∴OE=OF；

（2）当O为AC中点时，AECF为矩形

∵EO=OF，OA=OC

∴AECF为平行四边形

又∵CE、CF为△ABC内外角的平分线

∴∠EOF=90°，

∴AECF为矩形.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】阅读下面的推理过程，在括号内填上推理的依据，如图：

∵∠1+∠2=180°，∠2+∠4=180°(已知)

∴∠1=∠4( )

∴c∥a( )

又∵∠2+∠3=180°(已知 )

∠3=∠6( )

∴∠2+∠6=180°( )

∴a∥b( )

∴c∥b( )

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某学校对学生的暑假参加志愿服务时间进行抽样调查，将收集的数据分成A、B、C、D、E五组进行整理，并绘制成如下的统计图表（图中信息不完整）．

请结合以上信息解答下列问题

（1）求a、m、n的值．

（2）补全“人数分组统计图①中C组的人数和图②A组和B组的比例值”．

（3）若全校学生人数为800人，请估计全校参加志愿服务时间在30≤x＜40的范围的学生人数．

分组统计表

组别	志愿服务时间 x（时）	人数
A	0≤x＜10	a
B	10≤x＜20	40
C	20≤x＜30	m
D	30≤x＜40	n
E	x≥40	16

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知如图1，抛物线y=﹣x2﹣x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC

（1）求出直线AD的解析式；

（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；

（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，将边长为的菱形ABCD纸片放置在平面直角坐标系中．已知∠ABO=45°．

（1）求出点B、C的坐标；

（2）设边AB沿y轴对折后的对应线段为AB′，求出点B′的坐标及线段CB′的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：

成绩x/分	频数	频率
50≤x＜60	10	0.05
60≤x＜70	30	0.15
70≤x＜80	40	n
80≤x＜90	m	0.35
90≤x≤100	50	0.25

请根据所给信息，解答下列问题：

(1)m＝　　，n＝　　；

(2)请补全频数分布直方图；

(3)若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB=AC，∠BAC=90°，AH⊥BC于点H，过点C作CD⊥AC，连接AD，点M为AC上一点，且AM=CD，连接BM交AH于点N，交AD于点E．

（1）若AB=3，AD=，求△BMC的面积；

（2）点E为AD的中点时，求证：AD=BN ．

查看答案和解析>>

科目：初中数学 来源： 题型：

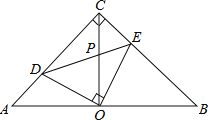
【题目】如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D，E分别在直角边AC，BC上，且∠DOE=90°，DE交OC于点P．则下列结论：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面积等于四边形CDOE面积的2倍；(4)OD=OE．其中正确的结论有( )